Question

【题目】在△ABC中，点E、F分别在BC、AB边上，且∠BEF+∠BFE﹣∠B＝∠A．

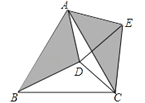
（1）如图1，求证：AB＝AC；

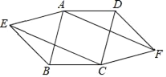
（2）如图2，延长EF交CA的延长线于D，点G是线段CE上一点，且∠CDE＝∠BDG＝90°，若∠BFE＝2∠DBA，求∠DGB的度数．

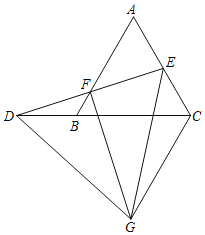
（3）如图3，在（2）的条件下，EG＝AC，CD＝8，求△BDG的面积．

Answer 1

【答案】（1）见解析；（2）45°；（3）16

【解析】

（1）由三角形内角和定理可得∠B＝∠C，可证AB＝AC；

（2）由余角的性质和三角形外角性质可得∠DBA＝∠BDE＝∠CDG，由直角三角形的性质可求解；

（3）如图3中，作DH⊥BC于H，GP∥AB交AC于P，GN⊥BC交AC于N，作AT⊥AB交BD的延长线于T，连接EN．利用全等三角形的性质想办法证明CN＝2NG，推出∠C＝30°即可解决问题．

解：（1）如图1中，

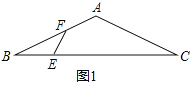
∵∠BEF+∠BFE﹣∠B＝∠A，

∴∠BEF+∠BFE＝∠A+∠B，

∵∠BEF+∠BFE+∠B＝∠A+∠B+∠C＝180°，

∴∠B＝∠C，

∴AB＝AC．

（2）如图2中，

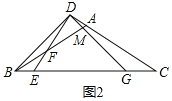
∵∠CDE＝∠BDG＝90°，

∴∠BDE＝∠CDG，

∵∠BFE＝2∠DBA＝∠DBA+∠BDE，

∴∠DBA＝∠BDE＝∠CDG，

∵∠ABC＝∠ACB，

∴∠ABC+∠DBA＝∠ACB+∠CDG，

∴∠DBG＝∠DGB，且∠BDG＝90°，

∴∠DGB＝∠DBG＝45°．

（3）如图3中，作DH⊥BC于H，GP∥AB交AC于P，GN⊥BC交AC于N，作AT⊥AB交BD的延长线于T，连接EN．

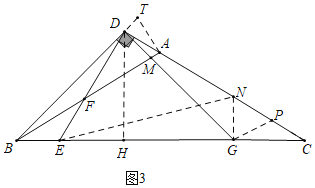
∵AB∥PG，

∴∠BAD＝∠DPG，∠PGC＝∠ABC，

∵AB＝AC，

∴∠ABC＝∠C＝∠PGC，

∴PG＝PC，

∵∠DBA＝∠GDP，DB＝DG，

∴△DBA≌△DGP（AAS），

∴AD＝PG＝PC，

∵∠PCG+∠CNG＝90°，∠PGC+∠PGN＝90°，

∴∠PNG＝∠PGN，

∴PG＝PN＝PC，

∵∠EGN＝∠EDN＝90°，

∴D，E，G，N四点共圆，

∴∠NEG＝∠GDN＝∠ABT，

∵∠EGN＝∠BAT＝90°，AB＝AC＝EG，

∴△BAT≌△EGN（ASA），

∴AT＝NG，

∵∠T+∠ABD＝90°，∠ADT+∠BDF＝90°，∠ABD＝∠BDF，

∴∠T＝∠ADT，

∴AD＝AT＝GN＝PC＝PN，

∴CN＝2GN，

∴∠C＝30°，

∵DH⊥BC，

∴∠DHC＝90°，

∴DH＝CD＝4，

∵△BGD是等腰直角三角形，DH⊥BG，

∴BH＝HG，

∴BG＝2DH＝8，

∴S△BGD＝BGDH＝×8×4＝16．