Question

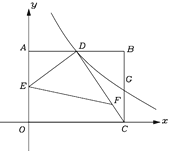
【题目】如图，平面直角坐标系中，矩形OABC的顶点B在第一象限，点C在x轴上，点A在y轴上，D、E分别是AB，OA中点．过点D的双曲线与BC交于点G．连接DC，F在DC上，且DF：FC=3:1,连接DE，EF．若△DEF的面积为6，则k的值为（　　）．

A. B. C. 6 D. 10

Answer 1

【答案】B

【解析】试题解析：设矩形OABC中OA=2a，AB=2b，

∵D、E分别是AB，OA中点，

∴点D（b，2a）、E（0，a），

如图，过点F作FP⊥BC于点P，延长PF交OA于点Q，

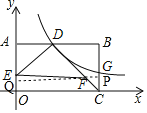
∵四边形OABC是矩形，

∴∠QOC=∠OCP=∠CPQ=90°，

∴四边形OCPQ是矩形，

∴OQ=PC，PQ=OC=2b，

∵FP⊥BC、AB⊥BC，

∴FP∥DB，

∴△CFP∽△CDB，

∴，即，

可得CP=，FP=，

则EQ=EO-OQ=a-=，FQ=PQ-PF=2b-=，

∵△DEF的面积为6，

∴S梯形ADFQ-S△ADE-S△EFQ=6，

即（b+）-b-×=6，

可得ab=，

则k=2ab=.

故选：B