题目内容
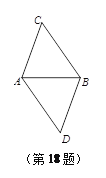
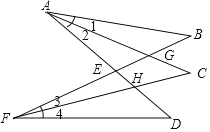
【题目】如图，AC，FC分别平分∠BAD，∠BFD，且分别与FB，AD相交于点G，H，已知∠B=40°，∠D=50°，求∠C的度数．
【答案】45°．
【解析】
由三角形内角和定理得出∠1-∠3=∠C-∠B，同理，∠2-∠4=∠D-∠C，由角平分线定义得出∠1=∠2，∠3=∠4，得出∠C-∠B=∠D-∠C，即可得出∠C的度数．
∵∠B+∠1+∠AGB=180°，∠C+∠3+∠CGF=108°，∠AGB=∠CGF
∴∠B+∠1=∠C+∠3，
∴∠1﹣∠3=∠C﹣∠B，
同理可得：∠2﹣∠4=∠D﹣∠C．
∵AC，FC分别平分∠BAD，∠BFD，
∴∠1=∠2，∠3=∠4，
∴∠C﹣∠B=∠D﹣∠C，
∴∠C
(∠B+∠D)×(40°+50°)=45°．
练习册系列答案
相关题目
