题目内容
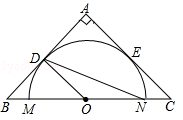
在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则∠MND的度数为 °．
22.5°
试题分析：利用等腰直角三角形的性质，求出∠B=∠C=45°，利用切线的性质，求出∠ODB=90°.
又∵∠BOD=∠OND+∠ODN ∵OD="ON," ∴∠OND=∠ODN=22.5°
试题解析：∵等腰直角三角形ABC∴∠A="90°" AB=AC ∴∠B=∠C=45°
又∵AB与⊙O相切于点D，∴∠ODB="90°" ∴∠DOB=45°又∵∠BOD=∠OND+∠ODN
又∵OD=ON ∴∠OND=∠ODN=22.5°
练习册系列答案
相关题目
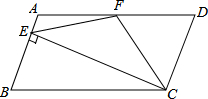
，试在AE上确定一点G，使△ABG≌△DAF．请你写出两种确定点G的方案，并就其中一种方案的具体作法证明△ABG≌△DAF．
，求△CAF的面积.
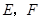为
上两点，且
，
．
； 
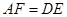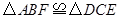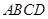是矩形．
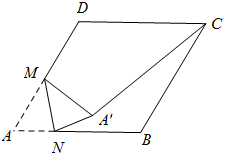
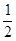∠BCD，（2）EF=CF；（3）SΔBEC=2SΔCEF；（4）∠DFE=3∠AEF
