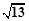题目内容
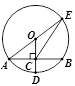
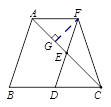
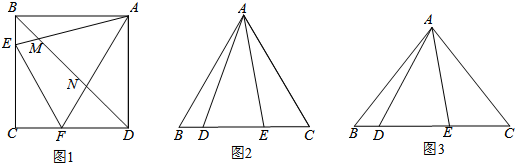
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF= ,求△CAF的面积.
,求△CAF的面积.

(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=
 ,求△CAF的面积.
,求△CAF的面积.
(1)证明见解析;(2)3.
试题分析:(1)根据平行四边形的定义即可证得.
(2)由平行四边形的性质得AF=BD=2,过点F作FG⊥AC于G点,从而由等腰直角三角形的性质得AG=GF=
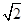 ,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=
,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=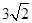 ,从而求得△CAF的面积.
,从而求得△CAF的面积.试题解析:(1)∵点D、E分别是边BC、AC的中点,∴DE∥AB.
∵AF∥BC,
∴四边形ABDF是平行四边形.
(2)如图,过点F作FG⊥AC于G点.
∵BC=4,点D是边BC的中点,∴BD=2.
由(1)可知四边形ABDF是平行四边形,∴AF=BD=2.
∵∠CAF=45°,∴AG=GF=
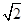 .
.在Rt△FGC中,∠FGC=90°, GF=
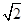 ,CF=
,CF= ,
,∴GC=
 .
.∴AC=AG+GC=
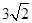 .
.∴
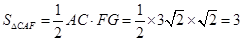 .
.

练习册系列答案
相关题目
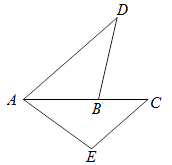
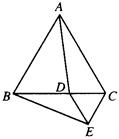
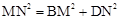 ,请证明这个等量关系;
,请证明这个等量关系;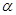 ,(0°<
,(0°<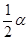 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: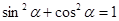 】
】
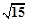 (B)8 (C)2
(B)8 (C)2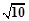 (D)2
(D)2