题目内容
【题目】如图,在平面直角坐标系中,点A(2,3),抛物线G:y=x2-2x+c(c为常数)的顶点坐标为M,其对称轴与x轴相交于点N.
(1)若抛物线G经过点A,求出其解析式,并写出点M的坐标.
(2)若点B(x1,y1)和点C(x1+3,y2)在抛物线G上,试比较y1,y2的大小.
(3)连接OM,若45°≤∠MON≤60°,请直接写出c的取值范围.
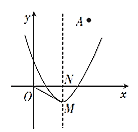
【答案】(1)(1,2)(2)当x>-![]() 时,y2>y1;当x=-
时,y2>y1;当x=-![]() 时,y2=y1;当x<-
时,y2=y1;当x<-![]() 时,y2<y1;(3)2≤c≤1+
时,y2<y1;(3)2≤c≤1+![]() 或1-
或1-![]() ≤c≤0
≤c≤0
【解析】
(1)把点A代入抛物线解析式求出c的值 ,得到抛物线的解析式进行配方即可得到M的坐标;
(2)先确定抛物线的对称轴,再将点B与点C分三种位置关系讨论求解即可;
(3)分别求出∠MON=45°时和∠MON=60°时c的值,即可求出45°≤∠MON≤60°时,c的取值范围.
把A(2,3)代入抛物线得4-4+c=3,
解得c=3,
∴y=x2-2x+3=(x-1)2+2
∴M(1,2);
(2)∵y=x2-2x+c,
∴对称轴为:x=1,
∴当x≤1时,y随x的增大而减小,当x≥1时,y随x的增大而增大,
①当B、C都在对称轴左侧时,x1+3≤1即x1≤-2时,y1>y2;
②当B、C都在对称轴右侧时,x1≥1时,y1<y2;
③当B在对称轴左侧、C在对称轴右侧时,x1<1且x1+3>1,
∴-2<x1<1
点B关于x=1的对称点为(2-x1,y1)
当2-x1<x1+3时,x1>-![]() ,y1<y2,
,y1<y2,
当2-x1>x1+3时,x1<-![]() ,y1>y2,
,y1>y2,
当2-x1=x1+3时,x1=-![]() ,y1=y2,
,y1=y2,
综上所述,
当x>-![]() 时,y2>y1;当x=-
时,y2>y1;当x=-![]() 时,y2=y1;当x<-
时,y2=y1;当x<-![]() 时,y2<y1;
时,y2<y1;
(3)∵y=x2-2x+c=(x-1)2+c-1,
∴顶点坐标为M(1,c-1),
∵对称轴与x轴交于点N,
∴N(1,0)
∴ON=1,
当∠MON=45°时,在Rt△MON中,![]() ,
,
∴|c-1|=1,
∴c=2或c=0;
当∠MON=60°时,在Rt△MON中,![]() ,
,
∴|c-1|=![]() ,
,
∴c=![]() +1或c=1-
+1或c=1-![]() ,
,
∴当45°≤∠MON≤60°时,2≤c≤1+![]() 或1-
或1-![]() ≤c≤0.
≤c≤0.