Question

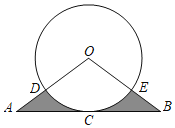
【题目】如图，AB与⊙O相切于点C，OA、OB分别交⊙O于点D、E、弧CD＝弧CE

(1)求证：∠A＝∠B.

(2)已知AC＝2，OA＝4，求阴影部分的面积.(结果保留根号和π)

Answer 1

【答案】(1)证明见解析；(2)4﹣π.

【解析】

(1)连接OC，根据切线的性质求出∠OCA＝∠OCB＝90°，根据弧CD＝弧CE推出∠AOC＝∠BOC，再根据三角形的内角和定理求出即可；

(2)求出∠AOB的度数和线段OC长，再根据三角形面积公式和扇形的面积公式求出即可.

(1)证明：连接OC，

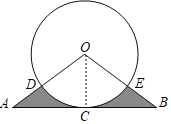
∵弧CD＝弧CE，

∴∠AOC＝∠BOC，

∵AB与⊙O相切于点C，

∴OC⊥AB，

∴∠OCA＝∠OCB＝90°，

∵∠A＝180°﹣∠OCA﹣∠AOC，∠B＝180°﹣∠OCB﹣∠BOC，

∴∠A＝∠B；

(2)解：∵∠A＝∠B，

∴OA＝OB，

∵OC⊥AB，

∵AC＝2，OA＝4，

∴BC＝AC＝2，OA＝OB＝4，AB＝4，

由勾股定理得：OC＝＝2，

∴OA＝2OC，

∴∠A＝30°，

∴∠AOC＝60°，

即∠AOB＝120°，

∴阴影部分的面积S＝S△AOB﹣S扇形DOE＝4×2﹣＝4﹣π.