Question

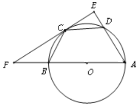
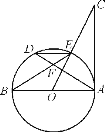
【题目】如图，AB是⊙O的直径，AD是弦，OC垂直AD于F交⊙O于E，连结DE，BE，且∠C＝∠BED．

(1)求证：AC是⊙O的切线；

(2)若OA＝10，AD＝16，求AC的长．

Answer 1

【答案】（1）见解析；（2）AC＝．

【解析】

（1）首先证明∠BAD=∠C，然后证明∠C+∠AOC=90°，即可证得∠OAC=90°，即OA⊥AC，从而得证；
（2）根据垂径定理和勾股定理求出OF的长，再根据△OAF∽△OCA，得出比例式，从而求出AC的长．

解：(1)证明：∵∠BED＝∠BAD，∠C＝∠BED，

∴∠BAD＝∠C．

∵OC⊥AD于点F，

∴∠BAD＋∠AOC＝90°，

∴∠C＋∠AOC＝90°，

∴∠OAC＝90°．

∴OA⊥AC，

∴AC是⊙O的切线．

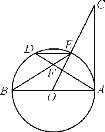
(2)∵OC⊥AD于点F，

∴AF＝AD＝8，在Rt△OAF中，OF＝＝6．

∵∠AOF＝∠AOC，∠OAF＝∠C，

∴△OAF∽△OCA，

∴=，∴

∴AC＝．