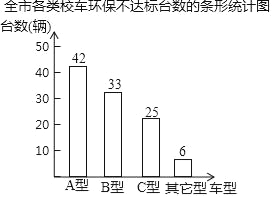
题目内容
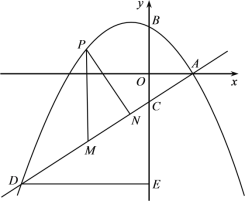
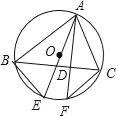
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
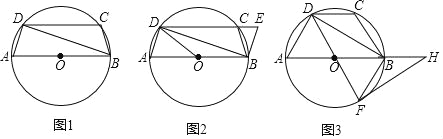
(1)求证:AB∥CD;
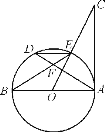
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)由弧AD=弧BC,根据同弧让所对的圆周角相等得∠ABD=∠BDC得AB∥CD;
(2)由∠BCE=∠CBA=∠DAO得∠CBE=2∠ABD且∠AOD=2∠ABD;从而得到△AOD∽△CBE,根据相似比得出结果;
(3)要证FH是⊙O的切线,只须证出DF⊥FH即可,作出辅助线是本题的关键.
解:(1)证明:圆内接四边形ABCD,AD=BC,
∴弧AD=弧BC,∴∠ABD=∠BDC
∴AB∥CD
(2)由(1)知,∠BCE=∠CBA=∠DAO,
∵∠CBE=2∠ABD且∠AOD=2∠ABD
∴△AOD∽△CBE
∴![]()
∴![]()
(3)作FM⊥AH于M,
∵∠ADB=∠AFB=∠DAF=90°
∴四边形AFBD是矩形,
∴FH=BD=AF
∴AM=HM,OM=BM
∴OF=BF=OD
∴∠FOH=60°,∠OHF=30°
∠DFH=90°
又∵DF是⊙O的直径,
∴FH是⊙O的切线.

练习册系列答案
相关题目