Question

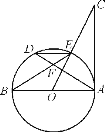
【题目】如图，AB是⊙O的直径，C,D在⊙O上，且BC=CD,过C作CE⊥AD,交AD延长线于E，交AB延长线于F点，

（1）求证：EF是⊙O的切线；

（2）若AB=4ED，求cos∠ABC的值.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）要证EF是⊙O的切线，只要证∠OCE=90°，根据OC=OA得到∠OCA=∠OAC，再证∠OCA=∠EAC，从而证∠OCA+∠ECA=90°；

（3）先证△CDE∽△ABC得到对应边成比例，由AB=4DE，BC=CD得到BC=AB，从而求出cos∠ABC=．

（1）证明：连接OC、AC
∵CE⊥AD
∴∠EAC+∠ECA=90°
∵OC=OA
∴∠OCA=∠OAC
又∵BC=CD
∴∠OAC=∠EAC
∴∠OCA=∠EAC
∴∠ECA+∠OCA=90°
∴EF是⊙O的切线．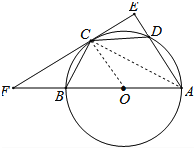

（2）解：∵EF是⊙O的切线
∴∠ECD=∠EAC
又∵BC=CD
∴∠EAC=∠BAC
∴∠ECD=∠BAC
又∵AB是直径
∴∠BCA=90°
在△BAC和△DCE中
∠BCA=∠DEC=90°
∠ECD=∠CAB
∴△CDE∽△ABC
∴
又∵AB=4DE，CD=BC
∴

.