ΧβΡΩΡΎ»ί
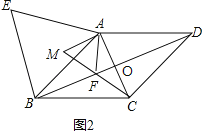
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΝβ–ΈABCD÷–Θ§Ε‘Ϋ«œΏAC”κBDœύΫΜ”ΎΒψOΘ§AB=13Θ§BD=24Θ§‘ΎΝβ–ΈABCDΒΡΆβ≤Ω“‘ABΈΣ±ΏΉςΒ»±Ώ»ΐΫ«–Έ ABEΘ°ΒψF «Ε‘Ϋ«œΏBD…œ“ΜΕ·ΒψΘ®ΒψF≤Μ”κΒψB÷ΊΚœΘ©Θ§ΫΪœΏΕΈAF»ΤΒψAΥ≥ ±’κΖΫœρ–ΐΉΣ60ΓψΒΟΒΫœΏΕΈAMΘ§Ν§Ϋ”FMΘ°

Θ®1Θ©«σAOΒΡ≥ΛΘΜ
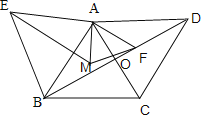
Θ®2Θ©»γΆΦ2Θ§Β±ΒψF‘ΎœΏΕΈBO…œΘ§«“ΒψMΘ§FΘ§C»ΐΒψ‘ΎΆ§“ΜΧθ÷±œΏ…œ ±Θ§«σ÷ΛΘΚAC=![]() AMΘΜ
AMΘΜ
Θ®3Θ©Ν§Ϋ”EMΘ§»τΓςAEMΒΡΟφΜΐΈΣ40Θ§«κ÷±Ϋ”–¥≥ωΓςAFMΒΡ÷ή≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓΔ5ΘΜΘ®2Θ©ΓΔ÷ΛΟςΙΐ≥ΧΦϊΫβΈωΘΜΘ®3Θ©ΓΔ3![]()
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΓΔ‘ΎRTΓςOAB÷–Θ§άϊ”ΟΙ¥Ι…Ε®άμOA=![]() «σΫβΘΜΘ®2Θ©ΓΔ”…ΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§«σ≥ωΓςAFMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΓœM=ΓœAFM=60ΓψΘ§‘Ό«σ≥ωΓœMAC=90ΓψΘ§‘ΎRtΓςACM÷–tanΓœM=
«σΫβΘΜΘ®2Θ©ΓΔ”…ΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§«σ≥ωΓςAFMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΓœM=ΓœAFM=60ΓψΘ§‘Ό«σ≥ωΓœMAC=90ΓψΘ§‘ΎRtΓςACM÷–tanΓœM=![]() Θ§«σ≥ωACΘΜΘ®3Θ©ΓΔ«σ≥ωΓςAEMΓ’ΓςABFΘ§άϊ”ΟΓςAEMΒΡΟφΜΐΈΣ40«σ≥ωBFΘ§‘Ύάϊ”ΟΙ¥Ι…Ε®άμAF=
Θ§«σ≥ωACΘΜΘ®3Θ©ΓΔ«σ≥ωΓςAEMΓ’ΓςABFΘ§άϊ”ΟΓςAEMΒΡΟφΜΐΈΣ40«σ≥ωBFΘ§‘Ύάϊ”ΟΙ¥Ι…Ε®άμAF=![]() =
=![]() Θ§ΒΟ≥ωΓςAFMΒΡ÷ή≥ΛΈΣ3
Θ§ΒΟ≥ωΓςAFMΒΡ÷ή≥ΛΈΣ3![]() Θ°
Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΔΓΏΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§
ΓύACΓΆBDΘ§OB=OD=![]() BDΘ§
BDȧ
ΓΏBD=24Θ§
ΓύOB=12Θ§
‘ΎRtΓςOAB÷–Θ§
ΓΏAB=13Θ§
ΓύOA=![]() =5Θ°
=5Θ°
Θ®2Θ©ΓΔ»γΆΦ2Θ§
ΓΏΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§
ΓύBD¥Ι÷±ΤΫΖ÷ACΘ§
ΓύFA=FCΘ§ΓœFAC=ΓœFCAΘ§
”…“―÷ΣAF=AMΘ§ΓœMAF=60ΓψΘ§
ΓύΓςAFMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœM=ΓœAFM=60ΓψΘ§
ΓΏΒψMΘ§FΘ§C»ΐΒψ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§
ΓύΓœFAC+ΓœFCA=ΓœAFM=60ΓψΘ§
ΓύΓœFAC=ΓœFCA=30ΓψΘ§
ΓύΓœMAC=ΓœMAF+ΓœFAC=60Γψ+30Γψ=90ΓψΘ§
‘ΎRtΓςACM÷–ΓΏtanΓœM=![]() Θ§
Θ§
Γύtan60Γψ=![]() Θ§
Θ§
ΓύAC=![]() AMΘ°
AMΘ°
Θ®3Θ©ΓΔ»γΆΦΘ§Ν§Ϋ”EMΘ§
ΓΏΓςABE «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύAE=ABΘ§ΓœEAB=60ΓψΘ§
”…Θ®2Θ©÷ΣΓςAFMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύAM=AFΘ§ΓœMAF=60ΓψΘ§
ΓύΓœEAM=ΓœBAFΘ§
‘ΎΓςAEMΚΆΓςABF÷–Θ§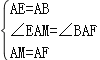 Θ§
Θ§
ΓύΓςAEMΓ’ΓςABFΘ®SASΘ©Θ§
ΓΏΓςAEMΒΡΟφΜΐΈΣ40Θ§ΓςABFΒΡΗΏΈΣAO
Γύ![]() BFAO=40Θ§BF=16Θ§
BFAO=40Θ§BF=16Θ§
ΓύFO=BF©¹BO=16©¹12=4
AF=![]() =
=![]() Θ§
Θ§
ΓύΓςAFMΒΡ÷ή≥ΛΈΣ3![]() Θ°
Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ