题目内容
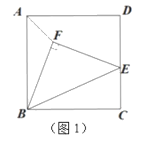
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,对称轴为直线
,对称轴为直线![]() ,顶点为
,顶点为![]() .
.
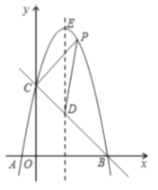
(1)求该二次函数的解析式;
(2)经过![]() 、
、![]() 两点的直线交抛物线的对称轴于点
两点的直线交抛物线的对称轴于点![]() ,点
,点![]() 为直线
为直线![]() 上方抛物线上的一动点,当点
上方抛物线上的一动点,当点![]() 在什么位置时,
在什么位置时,![]() 的面积最大?并求此时点
的面积最大?并求此时点![]() 的坐标及
的坐标及![]() 的最大面积;
的最大面积;
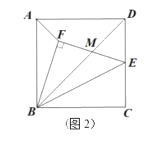
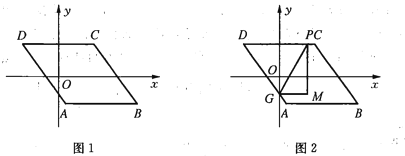
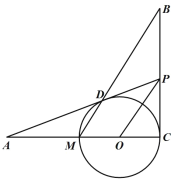
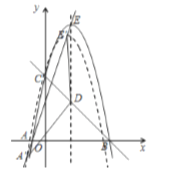
(3)如图,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() 平移后的对应点为
平移后的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 是否能为等腰三角形?若能,请求出所有符合条件的点
是否能为等腰三角形?若能,请求出所有符合条件的点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
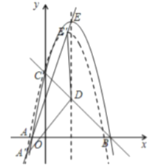
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() ;(3)存在,
;(3)存在,![]() ,
, ,
,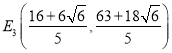 ,
,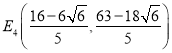 .
.
【解析】
(1)由对称性求得A点坐标, 再分别将点![]() 的坐标代入二次函数的解析式
的坐标代入二次函数的解析式![]() ,解方程组求出
,解方程组求出![]() 的值即可.
的值即可.
(2)由B,C两点得到直线BC的函数解析式,从而得到直线BC与对称轴的交点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,用含m的式子分别表示出PQ,
,用含m的式子分别表示出PQ,![]() ,得到
,得到![]() ,
,![]() ,进而转化为二次函数的最值问题来解决即可.
,进而转化为二次函数的最值问题来解决即可.
(3)由题可得![]() ,
,![]() ,故可得
,故可得![]() 的解析式为
的解析式为![]() ,设
,设![]() 其中(
其中(![]() ),则由平移的规律得
),则由平移的规律得![]() ,又
,又![]() ,根据平面上两点间的距离公式分别表示出
,根据平面上两点间的距离公式分别表示出![]() ,
,![]() ,
,![]() ,若
,若![]() 能为等腰三角形,则分三种情况:①若
能为等腰三角形,则分三种情况:①若![]() ,②若
,②若![]() ,若
,若![]() ,分别建立方程求解即可.
,分别建立方程求解即可.
(1)解:由对称性知点![]() ,
,
把![]() ,
,![]() ,
,![]() 代入得
代入得
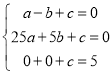 解得
解得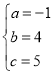
∴二次函数解析式为![]()
(2)
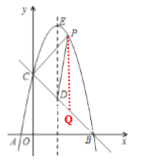
解:由题可得![]() 为
为![]() ,
,![]()
过![]() 作
作![]() 轴交
轴交![]() 于
于![]()
设![]() ,则
,则![]()
∴![]()
∴![]()
即:![]()
∵![]() ∴
∴![]() 有最大值
有最大值
当![]() 时,
时,![]()
此时,![]()
(3)解:由题可得![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() ,
,
设![]() 其中(
其中(![]() ),
),
则![]() ,
,![]() ,
,
![]() ,
,![]()
①若![]() ,则
,则![]()
得![]() ∴
∴![]()
②若![]() ,则
,则![]()
得![]() 或
或![]() (舍)∴
(舍)∴
③若![]() ,则
,则![]()
得![]() 或
或![]()
∴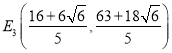 ,
,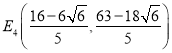
综上所述,存在![]() ,
, ,
,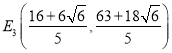 ,
,
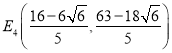 使
使![]() 为等腰三角形
为等腰三角形

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目