题目内容
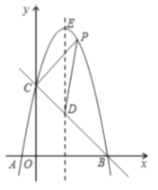
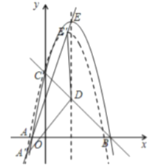
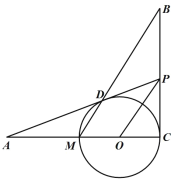
【题目】如图,已知BCAC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAOAMAP,连接OP.
(1)证明:MD//OP;
(2)求证:PD是⊙O的切线;
(3)若AD24,AMMC,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明,然后利用平行线的判定定理即可.
(2)欲证明PD是⊙O的切线,只要证明OD⊥PA即可解决问题;
(3)连接CD.由(2)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,![]() ,可得
,可得![]() ,推出
,推出![]() ,推出
,推出![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,再利用全等三角形的性质求出MD即可解决问题;
,再利用全等三角形的性质求出MD即可解决问题;
(1)证明:连接![]() 、
、![]() 、
、![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
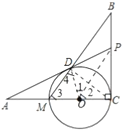
(3)连接![]() .由(1)可知:
.由(1)可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
【题目】甲、乙人5场10次投篮命中次数如图
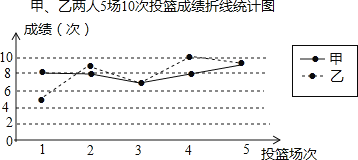
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)