题目内容
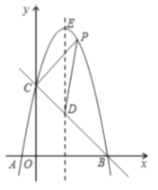
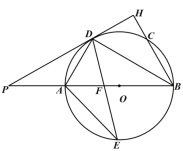
【题目】如图,![]() 的直径
的直径![]() ,点
,点![]() 为
为![]() 的延长线上一点,直线
的延长线上一点,直线![]() 切
切![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() 交
交![]() 于点
于点![]() ,连接
,连接 ![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 的长;
的长;
(3)![]() 是
是![]() 上的一动点,
上的一动点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?如果存在,请证明你的结论,并求
?如果存在,请证明你的结论,并求![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)连接OD易证OD∥BH,则∠ODB=∠DBH,然后根据等边对等角证明∠ODB=∠OBD,即可得证;
(2)证明四边形ODHG是矩形,得出OD=GH=5,DH=OG=4,BH=BG+GH=8,证明△POD∽△PBH,得出![]() ,即可得出答案;
,即可得出答案;
(3)当点E为AB弧的中点时,△ADE∽△FDB;则![]() ,由圆周角定理得出∠ADE=∠EDB,∠AED=∠ABD,证出△ADE∽△FDB,由弧长公式求出弧AE的长即可.
,由圆周角定理得出∠ADE=∠EDB,∠AED=∠ABD,证出△ADE∽△FDB,由弧长公式求出弧AE的长即可.
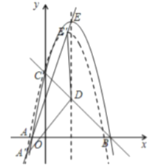
(1)证明:连接OD. 如图1所示:

∵PD是⊙O的切线,
∴OD⊥PD.
又∵BH⊥PD,
∴∠PDO=∠PHB=90°,
∴OD∥BH,
∴∠ODB=∠DBH.
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD=∠DBH,
∴BD平分∠ABH.
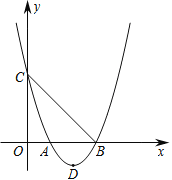
(2)解:过点O作OG⊥BC,G为垂足,如图2所示:

则BG=CG=![]() BC=3,
BC=3,
在Rt△OBG中,OG=![]() =4.
=4.
∵∠ODH=∠DHG=∠HGO=90°,
∴四边形ODHG是矩形.
∴OD=GH=5,DH=OG=4,BH=BG+GH=3+5=8.
∵OD∥BH,
∴△POD∽△PBH,
∴![]() ,即
,即![]() ,
,
解得:PA=![]() ;
;
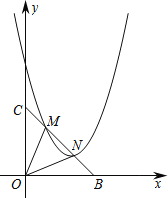
(3)解:存在,当点E为AB弧的中点时,△ADE∽△FDB,理由如下:
连接OE,如图3所示:

∵E是![]() 的中点,
的中点,
∴![]() ,
,
∴∠AOE=∠BOE=90°,∠ADE=∠EDB,
又∵∠AED=∠ABD,
∴△ADE∽△FDB,
![]() 的长
的长![]() .
.

练习册系列答案
相关题目