题目内容
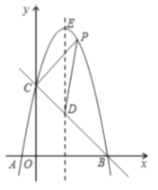
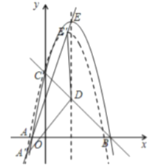
【题目】在正方形ABCD中,点E是直线CD上一动点,以BE为斜边向上方作等腰直角△BEF,连接AF,试求线段AF与DE的数量关系.
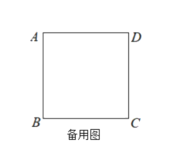
(1)小可同学进行探索:①将点E的位置特殊化,发现DE= ___ AF;
②点E运动过程中,∠BAF= ___ ;(填度数)
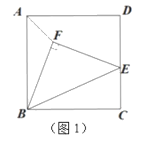
(2)如图1,当点E在线段CD上时,证明AF与DE的数量关系;
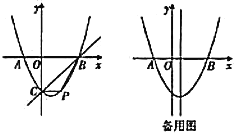
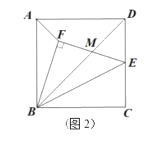
(3)如图2,当边EF被对角线BD平分时,求![]() 值.
值.
【答案】(1)①![]() ;②45°或135°;(2)
;②45°或135°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①当点E与点C重合、点F与点O重合时,可证得DE=![]() AF,∠BAF=45°;
AF,∠BAF=45°;
②当点E在CD延长线上时,利用两边对应成比例且夹角相等证得△ABF∽△DBE,即可求得∠BAF=∠BDE=135°;
(2)利用两边对应成比例且夹角相等证得△ABF∽△DBE,即可求得答案;
(3)利用(2)的结论证得![]() ,BF
,BF![]() ,则FE=
,则FE=![]() ,BE=
,BE=![]() ,求得BM
,求得BM![]()
![]() ,证得△MBE∽△EBD,得到
,证得△MBE∽△EBD,得到![]() ,即可求得BD和MD的长,从而求得答案.
,即可求得BD和MD的长,从而求得答案.
(1)①∵四边形ABCD是正方形,
∴OB=OC=![]() AC=
AC=![]() BD,∠BOC=90°,
BD,∠BOC=90°,
当点E与点C重合、点F与点O重合时,如图:
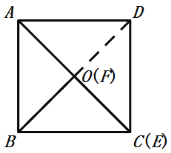
△BEF等腰直角三角形,
∴DE=AB=![]() AF,
AF,
②∠BAF=45°;
当点E在CD延长线上时,如图:
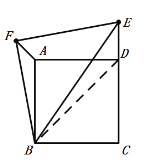
连接BD,
∵四边形ABCD是正方形
∴∠ABD=45°,
∴![]() ,
,
∵△BEF是等腰直角三角形,∠BFE=90°,
∴BF=FE,∠FBE=45°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴∠ABF+∠EBA =∠DBE+∠EBA =45°,
∴∠ABF=∠DBE,
∴△ABF∽△DBE,
∴∠BAF=∠BDE=∠ADB+∠ADE =45°+90°=135°,
故答案为:①DE=![]() AF,②∠BAF=45°或135°;
AF,②∠BAF=45°或135°;
(2)连接BD,

∵四边形ABCD是正方形
∴∠ABD=45°,
∴![]() ,
,
∵△BEF是等腰直角三角形,∠BFE=90°,
∴BF=FE,∠FBE=45°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴∠ABF+∠DBF =∠DBE+∠DBF=45°,
∴∠ABF=∠DBE,
∴△ABF∽△DBE,
∴![]() ,
,
∴![]() ;
;
(3)∵△ABF∽△EBD,
∴![]() ,
,
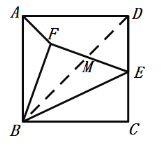
又∵∠MEB=∠BDE=45°,∠MBE=∠EBD,
∴△MBE∽△EBD,
∴![]() ,
,
令BF![]() ,
,
∴FE=![]() ,BE=
,BE=![]() ,
,
∵M是FE的中点,
∴FM=![]() ,
,
∴BM=![]()
![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
∴MD=BD-BM=![]() -
-![]() =
=![]() ,
,
∴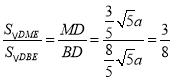 ,
,
∴![]() .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
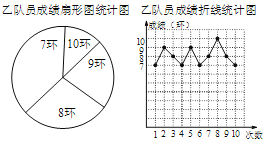
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
【题目】甲、乙人5场10次投篮命中次数如图
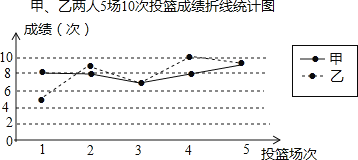
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)