Question

【题目】如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线y＝﹣x+m交折线OAB于点E．

（1）请写出m的取值范围 ；

（2）记△ODE的面积为S，求S与m的函数关系式．

Answer 1

【答案】（1）1＜m＜2.5；（2）S＝

【解析】

（1）利用一次函数图象上点的坐标特征可求出点D的坐标，根据点D横坐标的范围即可得出m的取值范围；
（2）分点E在线段OA上及点E在线段AB上时（与端点A、B不重合）两种情况考虑：①当点E在线段OA上时，利用一次函数图象上点的坐标特征可求出点E的坐标，由点E的横坐标≤3可得出此时m的取值范围，再利用三角形的面积公式可找出S关于m的函数关系式；②当点E在线段AB上时（与端点A、B不重合），此时1.5＜m＜2.5，利用一次函数图象上点的坐标特征可求出点E的坐标，结合点D、B的坐标即可得出CD、AE、BD、BE的长度，再根据S=S矩形OABC-S△OAE-S△OCD-S△BDE即可找出S关于m的函数关系式．综上即可得出结论．

解：（1）当y＝1时，有﹣x+m＝1，

∴x＝2m﹣2，

∴点D的坐标为（2m﹣2，1）．

∵点D是线段BC上的动点（与端点B、C不重合），

∴0＜2m﹣2＜3，

∴1＜m＜2.5．

故答案为：1＜m＜2.5．

（2）①当点E在线段OA上时，如图1所示．

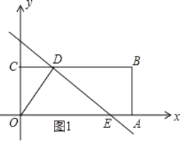
当y＝0时，有﹣x+m＝0，

∴x＝2m，

∴点E的坐标为（2m，0），

∴2m≤3，

∴此时1＜m≤1.5，S＝OE OC＝m；

②当点E在线段AB上时（与端点A、B不重合），此时1.5＜m＜2.5，如图2所示．

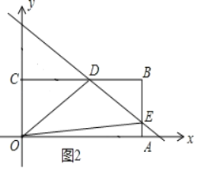
当x＝3时，y＝﹣x+m＝m﹣1.5，

∴点E的坐标为（3，m﹣1.5）．

∵点D的坐标为（2m﹣2，1），点B的坐标为（3，1），

∴CD＝2m﹣2，BD＝5﹣2m，AE＝m﹣1.5，BE＝2.5﹣m，

S＝S矩形OABC﹣S△OAE﹣S△OCD﹣S△BDE，

＝OAOC﹣OAAE﹣OCCD﹣BDBE，

＝3×1﹣×3（m﹣1.5）﹣（2m﹣2）﹣（5﹣2m）（2.5﹣m），

＝﹣m2+2.5m．

综上所述：S与m的函数关系式为S＝．