题目内容
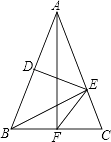
【题目】实践操作：在矩形ABCD中，AB＝4，AD＝3，现将纸片折叠，点D的对应点记为点P，折痕为EF（点E、F是折痕与矩形的边的交点），再将纸片还原．
初步思考：
（1）若点P落在矩形ABCD的边AB上（如图①）
①当点P与点A重合时，∠DEF＝ °；当点E与点A重合时，∠DEF＝ °；
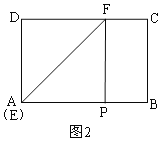
②当点E在AB上，点F在DC上时（如图②），
求证：四边形DEPF为菱形，并直接写出当AP＝3.5时的菱形EPFD的边长．
深入探究
（2）若点P落在矩形ABCD的内部（如图③），且点E、F分别在AD、DC边上，请直接写出AP的最小值 ．
拓展延伸
（3）若点F与点C重合，点E在AD上，线段BA与线段FP交于点M（如图④）．在各种不同的折叠位置中，是否存在某一情况，使得线段AM与线段DE的长度相等？若存在，请直接写出线段AE的长度；若不存在，请说明理由．
【答案】⑴①90；45 ②
（2）最小值为1 (3)
【解析】
（1）①当点P与点A重合时，如图1，画出图形可得结论；
当点E与点A重合时，如图2，则EF平分∠DAB；
②证明△DOF≌△POE（ASA）得DF=PE，根据一组对边平行且相等得：四边形DEPF是平行四边形，加上对角线互相垂直可得DEPF为菱形，
当AP=7时，设菱形的边长为x，根据勾股定理列方程得：62+（7-x）2=x2，求出x的值即可；
（2）如图4，当F与C重合，点P在对角线AC上时，AP有最小值，根据折叠的性质求CD=PC=4，由勾股定理求AC=5，所以AP=5-4=1；
（3）根据全等三角形的判定和性质以及勾股定理解答即可．
（1）①当点P与点A重合时，如图1，
∴EF是AD的中垂线，
∴∠DEF=90°，
当点E与点A重合时，如图2，
此时∠DEF=
∠DAB=45°，
故答案为：90°，45°；
②当点E在AB上，点F在DC上时，如图3，
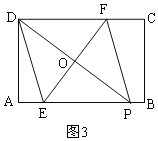
∵EF是PD的中垂线，
∴DO=PO，EF⊥PD，
∵四边形ABCD是矩形，
∴DC∥AB，
∴∠FDO=∠EPO，
∵∠DOF=∠EOP，
∴△DOF≌△POE（ASA），
∴DF=PE，
∵DF∥PE，
∴四边形DEPF是平行四边形，
∵EF⊥PD，
∴DEPF为菱形，
当AP=3.5时，设菱形的边长为x，则AE=3.5-x，DE=x，
在Rt△ADE中，由勾股定理得：AD2+AE2=DE2，
∴32+（3.5-x）2=x2，
x=，
∴当AP=3.5时，设菱形的边长为；
（2）若点P落在矩形ABCD的内部，且点E、F分别在AD、DC边上，如图4，
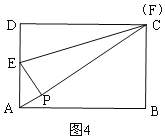
设DF=PF=x，则AF=
，当A，P，F在一直线上时，AP最小，最小值为x＝
，所以当x最大取4时，AP最小值为1；
（3）情况一：如图5，连接EM，
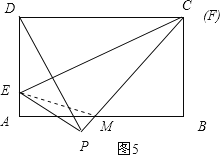
∵DE=EP=AM，
∴△EAM≌△MPE，
设AE=x，则AM=DE=3-x，则BM=x+1，
∵MP=EA=x，CP=CD=4，
∴MC=4-x，
∴（x+1）2+32=（4-x）2，
解得：x=.
故AE=.
