题目内容
【题目】如图,二次函数 ![]() 的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
的图象经过坐标原点,与x轴的另一个交点为A(-2,0).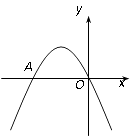
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
【答案】
(1)解:∵二次函数y=-x2+bx+c的图象经过坐标原点(0,0)
∴c=0.
又∵二次函数y=-x2+bx+c的图象过点A(-2,0)
∴-(-2)2-2b+0=0,
∴b=-2.
∴所求b、c值分别为-2,0
故二次函数解析式为:y=-x2-2x.
(2)解:存在一点P,满足S△AOP=3.
设点P的坐标为(x,-x2-2x)
∵S△AOP=3
∴ ![]() ×2×|-x2-2x|=3
×2×|-x2-2x|=3
∴-x2-2x=±3.
当-x2-2x=3时,此方程无解;
当-x2-2x=-3时,
解得 x1=-3,x2=1.
∴点P的坐标为(-3,-3)或(1,-3)
【解析】(1)抓住已知条件抛物线经过原点(0,0)和A(-2,0).将这两点坐标代入函数解析式,建立方程组,求解即可得到抛物线的解析式。
(2)由于点P在抛物线上,因此设点P的坐标为(x,-x2-2x),根据点A的坐标可求出OA=2,再根据S△AOP=3,建立方程,解方程求出x的值,即可得到点P的坐标。
【考点精析】通过灵活运用因式分解法和三角形的面积,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;三角形的面积=1/2×底×高即可以解答此题.

 口算能手系列答案
口算能手系列答案【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价 | 零售价 | |
餐桌 | a | 270 |
餐椅 | b | 70 |
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
![]() 求表中a,b的值;
求表中a,b的值;
![]() 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了![]() ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.