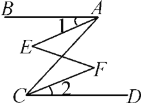
题目内容
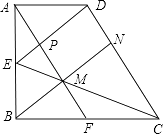
【题目】如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,则y与x之间的函数关系式为.
【答案】![]()
【解析】∵∠BAC=30°, AB=AC,
∴∠ACB=∠ABC= ![]() ,
,
∴∠ACE=∠ABD=180°-75°=105°,
∵∠DAE=105°,∠BAC=30°,
∴∠DAB+∠CAE=105°-30°=75°,
又∵∠DAB+∠ADB=∠ABC=75°,
∴∠ADB=∠CAE.
∴△ADB∽△EAC,
∴ ![]() ,即
,即 ![]() ,
,
∴ ![]() .
.
故答案为: ![]() .
.
根据AB=AC,易证∠ACE=∠ABD,再根据∠DAE=105°,∠BAC=30°,得出∠DAB+∠CAE=75°,由∠DAB+∠ADB=75°,得出∠ADB=∠CAE,就可证得△ADB∽△EAC,得出对应边成比例,即可求出y与x之间的函数关系式。

练习册系列答案
相关题目
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价 | 零售价 | |
餐桌 | a | 270 |
餐椅 | b | 70 |
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
![]() 求表中a,b的值;
求表中a,b的值;
![]() 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了![]() ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.