题目内容
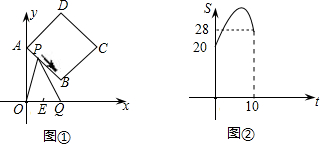
如图①,正方形ABCD的顶点A,B的坐标分别为(0,10),(8,4),顶点C,D在第一象限,点P从点A出发,沿正方形的边按逆时针方向匀速运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同速度运动,当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒.(1)求正方形ABCD的边长.
(2)当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(s)之间的函数图象为抛物线的一部分(如图②所示),求P,Q两点的运动速度.
(3)求(2)中面积S(平方单位)与时间t(s)的函数关系式及面积S取最大值时点P的坐标.
分析:(1)本题须先作BF⊥y轴于F.再求出FB和FA的值即可得出AB的长.
(2)本题须求出点P从点A运动到点B用了多少时间,再根据AB的长即可求出P、Q两点的运动速度.
(3)本题须先作PG⊥y轴于G,证出△AGP∽△AFB得出S=
OQ•OG,再把OQ•OG的值代入即可得出S=-
t2+
t+20
最后即可得出S有最大值时P点的坐标.
(2)本题须求出点P从点A运动到点B用了多少时间,再根据AB的长即可求出P、Q两点的运动速度.
(3)本题须先作PG⊥y轴于G,证出△AGP∽△AFB得出S=
| 1 |
| 2 |
| 3 |
| 10 |
| 19 |
| 5 |
最后即可得出S有最大值时P点的坐标.
解答: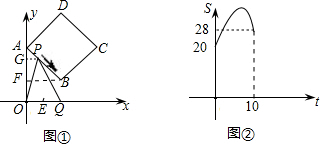 解:(1)作BF⊥y轴于F.
解:(1)作BF⊥y轴于F.
∵A(0,10),B(8,4)
∴FB=8,FA=6,
∴AB=10;
(2)∵点P从A点移动到B点时,△OPQ的面积为28,
由图2可知,当t=10时,s=28,
∴点P从点A运动到点B用了10s,
∵AB=10,
∴P、Q两点的运动速度均为每秒一个单位长度.
(3)作PG⊥y轴于G,则PG∥BF.
∴△AGP∽△AFB
∴
=
,即
=
∴GA=
t,OG=10-
t,
又∵OQ=4+t,
∴S=
OQ•OG,
=
(t+4)(10-
t),
即:S=-
t2+
t+20,
-
=-
=
,
且:
在0≤t≤10内,
∴当t=
时,S有最大值,此时GP=
t=
,
OG=10-
t=
,
∴P(
,
).
 解:(1)作BF⊥y轴于F.
解:(1)作BF⊥y轴于F.∵A(0,10),B(8,4)
∴FB=8,FA=6,
∴AB=10;
(2)∵点P从A点移动到B点时,△OPQ的面积为28,
由图2可知,当t=10时,s=28,
∴点P从点A运动到点B用了10s,
∵AB=10,
∴P、Q两点的运动速度均为每秒一个单位长度.
(3)作PG⊥y轴于G,则PG∥BF.
∴△AGP∽△AFB
∴
| GA |
| FA |
| AP |
| AB |
| GA |
| 6 |
| t |
| 10 |
∴GA=
| 3 |
| 5 |
| 3 |
| 5 |
又∵OQ=4+t,
∴S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 5 |
即:S=-
| 3 |
| 10 |
| 19 |
| 5 |
-
| b |
| 2a |
| ||
2×(-
|
| 19 |
| 3 |
且:
| 19 |
| 3 |
∴当t=
| 19 |
| 3 |
| 4 |
| 5 |
| 76 |
| 15 |
OG=10-
| 3 |
| 5 |
| 31 |
| 5 |
∴P(
| 76 |
| 15 |
| 31 |
| 5 |
点评:本题主要考查了二次函数的应用,在解题时要注意综合运用数形结合思想,灵活应用二次函数的图象和性质是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
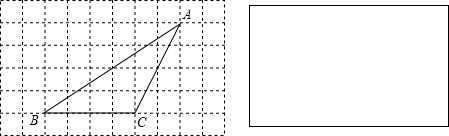
 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
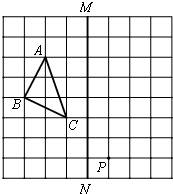
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)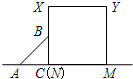 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
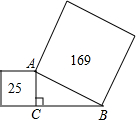 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )