题目内容
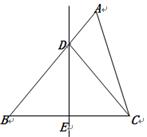
在 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.

(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
(1)通过“边角边”可得出△BEC≌△DFA (2)四边形AECF是矩形
试题分析:(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,BC=AD。
∵E、F分别是AB、CD的中点,∴BE=
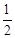 AB,DF=
AB,DF=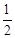 CD。
CD。∴BE=DF。∴△BEC≌△DFA(SAS)。
(2) 四边形AECF是矩形。证明如下:
∵四边形ABCD是平行四边形,∴AB∥CD,且AB=CD。
∵E、F分别是AB、CD的中点,∴AE=
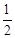 AB,CF=
AB,CF=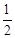 CD。
CD。∴AE∥CF,且AE=CF。∴四边形AECF是平行四边形。
又∵CA=CB,E是AB的中点,∴CE⊥AB,即∠AEC=900。
∴
 AECF是矩形。
AECF是矩形。点评:本题考查全等三角形、矩形,解答本题需要掌握全等三角形的证明方法,会证明两个三角形全等,熟悉矩形的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
;