题目内容
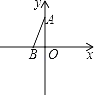
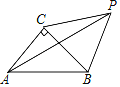
【题目】如图,AC=BC,∠CPB=45°,AC⊥BC,若S△APB=32,则PB的长为_____.
【答案】8
【解析】
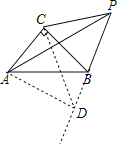
根据∠CPB=45°应构建直角三角形进行求解,如图,过点C作CD⊥CP交PB的延长线于点D,可求证△ACD≌△BCP(SAS),即可证AD=PB,AD为△APB的高,则可求PB的值.
解:如图,过点C作CD⊥CP交PB的延长线于点D,连接AD
∵∠CPB=45°,∠DCP=90°
∴△DCP为等腰直角三角形,
∴CP=CD
∵∠ACB=90°
∴∠ACD+∠DCB=∠DCB+∠PCB=90°
∴∠ACD=∠PCB
又∵△ACB为等腰直角三角形
∴AC=CB
∴在△ACD和△BCP中
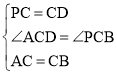 ,
,
∴△ACD≌△BCP(SAS)
∴∠ADC=∠CPB=45°,AD=PB
∵∠CDP=∠CPB=45°
∴∠ADB=90°
∴AD为△APB的高
∴S△APB=![]() ×AD×PB=
×AD×PB=![]() ×PB×PB=
×PB×PB=![]() PB2=32
PB2=32
∴PB2=64
∵PB>0
∴PB=8
故答案为8

练习册系列答案
相关题目