Question

【题目】如图所示，函数y1＝kx+b的图象与函数（x＜0）的图象交于A（a﹣2，3）、B（﹣3，a）两点．

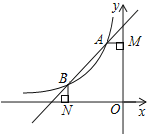
（1）求函数y1、y2的表达式；

（2）过A作AM⊥y轴，过B作BN⊥x轴，试问在线段AB上是否存在点P，使S△PAM＝3S△PBN？若存在，请求出P点坐标；若不存在，请说明理由．

Answer 1

【答案】（1），；（2）存在，P.

【解析】

（1）把A、B两点坐标代入直线AB解析式可求得A、B两点的坐标，再把B点坐标代入反比例函数解析式可求得k，可求得函数y2的表达式；

（2）设出P点坐标为（x，x＋4），根据三角形的面积关系可得到关于x的方程，可求得P点坐标．

解：（1）∵A、B两点在函数（x＜0）的图象上，

∴3（a﹣2）＝﹣3a＝m，

∴a＝1，m＝﹣3，

∴A（﹣1，3），B（﹣3，1），

∵函数y1＝kx+b的图象过A、B点，

∴，

解得k＝1，b＝4

∴y1＝x+4，y2＝；

（2）由（1）知A（﹣1，3），B（﹣3，1），

∴AM＝BN＝1，

∵P点在线段AB上，

∴设P点坐标为（x，x+4），其中﹣1≤x≤﹣3，

则P到AM的距离为hA＝3﹣（x+4）＝﹣x﹣1，P到BN的距离为hB＝3+x，

∴S△PBN＝BNhB＝×1×（3+x）＝（x+3），

S△PAM＝AMhA＝×1×（﹣x﹣1）＝﹣（x+1），

∵S△PAM＝3S△PBN，

∴﹣（x+1）＝（x+3），解得x＝﹣，且﹣1≤x≤﹣3，符合条件，

∴P（﹣，），

综上可知存在满足条件的点P，其坐标为（﹣，）．