Question

【题目】已知函数y＝x＋1，反比例函数y＝．

（1）当k为何值时，这两个函数的图象有两个交点？

（2）当k为何值时，这两个函数的图象没有交点？

（3）这两个函数的图象能否只有一个交点？若有，求出这个交点坐标；若没有，请说明理由．

Answer 1

【答案】（1）k＞－且k≠ 0；（2）k＜－；（3）k＝－，交点坐标为(－， )

【解析】试题分析：这两个函数的图象有两个交点，即联立后方程组有两个解；两个函数的图象没有交点，即联立后方程组无解；两个函数的图象有一个交点，即联立后方程组有两个相等的解据此联立两个函数的解析式，根据对称性解出答案即可；

试题解析：解：联立解析式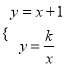： ，可得：x+1=，∵x≠0，∴x2+x﹣k=0，（1）若两个函数的图象有两个交点，则△=1+4k＞0，解得：k＞﹣且k≠0；

（2）若两个函数的图象没有交点，则△=1+4k＜0，解得：k＞﹣．

（3）两个函数的图象只有一个交点，则△=1+4k=0，解得：k=﹣，∴x2+x+=0．解得，x=﹣，代入y=x+1得，y=，∴这个交点坐标为（﹣， ）．