题目内容
【题目】如图![]() ,在长方形
,在长方形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 开始以
开始以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,点
运动,点![]() 从点
从点![]() 以
以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,如果
运动,如果![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到点
运动到点![]() 时,
时, ![]() 、
、![]() 同时停止运动.在运动过程中,是否存在
同时停止运动.在运动过程中,是否存在![]() 的值,使得
的值,使得![]() 、
、![]() 、
、![]() 的面积都相等,若存在,求出
的面积都相等,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(![]() )当运动
)当运动![]() 时,
时, ![]() 点停止运动,
点停止运动, ![]() 点以原速立即向
点以原速立即向![]() 点返回,在返回的过程中,
点返回,在返回的过程中, ![]() 是否能平分
是否能平分![]() ?若能,求出点
?若能,求出点![]() 运动的时间;若不能,请说明理由.
运动的时间;若不能,请说明理由.
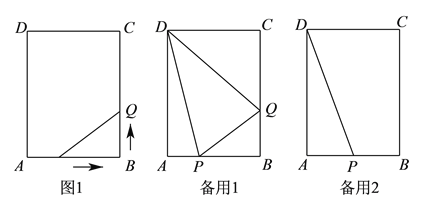
【答案】见解析.
【解析】试题分析:(1)根据题意,易求BP的长,再利用勾股定理求得PQ的长即可;(2)用t表示出![]() 和
和![]() ,根据面积相等列出方程,解方程即可解决问题;(3)若
,根据面积相等列出方程,解方程即可解决问题;(3)若![]() 平分
平分![]() ,作
,作![]() 于点
于点![]() (如图所示),利用HL证明
(如图所示),利用HL证明![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,再用AAS证明
,再用AAS证明![]() ≌
≌![]() ,设
,设![]() ,则
,则![]() ,
, ![]() .在
.在![]() 中,根据勾股定理列出方程,解方程求得x的值,继而求得t值.
中,根据勾股定理列出方程,解方程求得x的值,继而求得t值.
试题解析:
(![]() )
)![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() .
.
∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.
![]()
![]() .
.
若![]() .
.
即![]() .
.
解得![]() .
.
∴不存在.
(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() .
.
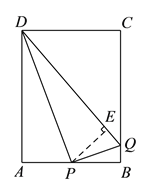
如图所示,若![]() 平分
平分![]() ,作
,作![]() 于点
于点![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
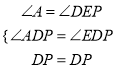 ,
,
∴![]() ≌
≌![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
![]() .
.
在![]() 中,
中, ![]() .
.
即![]() .
.
解得![]() .
.
∴![]() .
.
∴![]() 又走了
又走了![]() ,
,
∵原来运动![]() .
.
∴![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目