题目内容
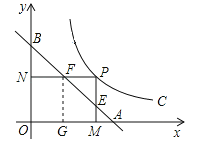
【题目】已知：如图，动点P在函数y＝
（x＞0）的图象上运动，PM⊥x轴于M，PN⊥y轴于N，线段PM、PN分别与直线AB：y＝－x＋1交于点E、F，且AFBE的值为1，则k为________．
【答案】
【解析】解：作FG⊥x轴，∵P的坐标为（a， 
），且PN⊥OB，PM⊥OA，∴N的坐标为（0， 
），M点的坐标为（a，0），∴BN=1﹣
，在直角三角形BNF中，∠NBF=45°（OB=OA=1，三角形OAB是等腰直角三角形），∴NF=BN=1﹣
，∴F点的坐标为（1﹣
， 
），同理可得出E点的坐标为（a，1﹣a），∴AF2=（1﹣1+
）2+（
）2=
，BE2=（a）2+（﹣a）2=2a2，∴AF2BE2=
2a2=1，k=
．故答案为： 
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +12 | ﹣10 | +16 | ﹣9 |
（1）根据记录的数据可知该厂星期六生产自行车______辆；
（2）根据记录的数据可知该厂本周实际生产自行车_____辆；
（3）产量最多的一天比产量最少的一天多生产自行车_____辆；
（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
