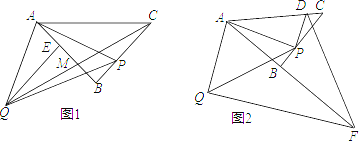
题目内容
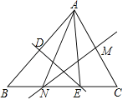
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
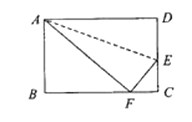
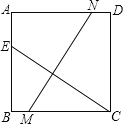
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
【答案】(1)证明见详解;(2)2;(3)式子值不变,理由见详解.
【解析】
(1)根据题目中的信息可以得到AQ=AP,∠QEA与∠ABP之间的关系,∠QAE与∠APB之间的关系,从而可以解答本题;
(2)由第一问中的两个三角形全等,可以得到各边之间的关系,然后根据题目中的信息找到PC与MB的关系,从而可以解答本题;
(3)作合适的辅助线,构造直角三角形,通过三角形的全等可以找到所求问题需要的边之间的关系,从而可以解答本题.
(1)证明:∵△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.
∴AP=AQ,∠ABQ=∠QEA=90°,∠QAE+∠BAP=∠BAP+∠APB=90°,
∴∠QAE=∠APB,
在△PAB和△AQE中,
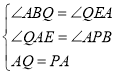
∴△PAB≌△AQE(AAS);
(2) ∵△PAB≌△AQE,
∴AE=PB,
∵AB=CB,
∴QE=CB.
在△QEM和△CBM中,
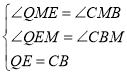
∴△QEM≌△CBM(AAS),
∴ME=MB,
∵AB=CB,AE=PB,PC=2PB,
∴BE=PC,
∵PC=2PB,
∴PC=2MB,
∴![]()
(3)式子![]() 的值不会变化.
的值不会变化.
如下图所示:作HA⊥AC交QF于点H,

∵QA⊥AP,HA⊥AC,AP⊥PD,
∴∠QAH+∠HAP=∠HAP+∠PAD=90°,∠AQH=∠APD=90°,
∴∠QAH=∠PAD,
∵△PAQ为等腰直角三角形,
∴AQ=AP,
在△AQH和△APD中,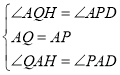
∴△AQH≌△APD(ASA),
∴AH=AD,QH=PD,
∵HA⊥AC,∠BAC=45°,
∴∠HAF=∠DAF,
在△AHF和△ADF中,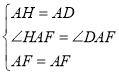
∴△AHF≌△ADF(SAS),
∴HF=DF,
∴![]()