题目内容
【题目】已知在四边形ABCD中,∠A=∠C=90°.

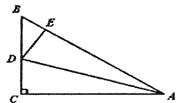
(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.
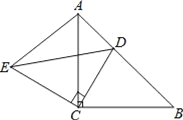
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
(3)如图3,若BE、DE分别六等分∠ABC、∠ADC的邻补角(即∠CBE=![]() ∠CBM,∠CDE=
∠CBM,∠CDE=![]() ∠CDN),则∠E= .
∠CDN),则∠E= .
【答案】(1)![]() ;(2)
;(2)![]() ∥
∥![]() ;(3)
;(3)![]() 60O
60O
【解析】
(1)如图1中,延长BE交FD的延长线于H.想办法证明∠DEH+∠EDH=90°即可;
(2)如图2中,连接BD,只要证明∠EDB+∠FBD=180°即可;
(3)利用结论:∠DCB=∠E+∠CBE+∠CDE即可解决问题;
解:(1)结论:BE⊥DF;
理由:如图1中,延长BE交FD的延长线于H.
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠CDN=180°,
∴∠ABC=∠CDN,
∵∠ABE=![]() ∠ABC,∠FDN=∠EDH=
∠ABC,∠FDN=∠EDH=![]() ∠CDN,
∠CDN,
∴∠ABE=∠EDH,
∵∠ABE+∠AEB=90°,∠AEB=∠DEH,
∴∠DEH+∠EDH=90°,
∴∠H=90°,
即BE⊥DF.
(2)结论:DE∥BF;
理由:如图2中,连接BD.
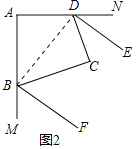
∵∠ABC+∠ADC=180°,∠MBC+∠ABC=180°,∠CDN+∠ADC=180°,
∴∠MBC+∠CDN=180°,
∵∠CBF=![]() ∠MBC,∠CDN=
∠MBC,∠CDN=![]() ∠CDN,
∠CDN,
∴∠CBF+∠CDE=90°,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∴∠EDB+∠FBD=∠CBF+∠CDE+∠CBD+∠CDB=180°,
∴DE∥BF.
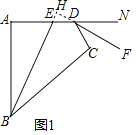
(3)如图3中,
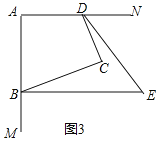
∵∠MBC+∠CDN=180°,
∴∠CDE+∠CBE=![]() (∠MBC+∠CDN)=30°,
(∠MBC+∠CDN)=30°,
∵∠DCB=∠E+∠CBE+∠CDE,
∴∠E=90°-30°=60°.
故答案为60°.