题目内容
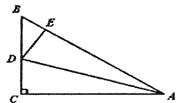
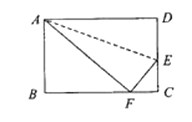
【题目】如图,一张长方形纸片宽AB=DC=8 cm,长BC=AD=10 cm,∠B=∠C=∠D=∠BAD=90°.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.
【答案】3
【解析】
首先根据勾股定理求出BF的长,进而求出FC的长;再次根据勾股定理,列出关于线段EF的方程,求出EF的长度,即可解决问题.
解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=10;DC=AB=8;
根据折叠的性质得AF=AD=10,EF=ED,
由勾股定理得:
BF2=AF2-AB2=102-82=36,
∴BF=6,CF=10-6=4;
由勾股定理得:
EF2=EC2+CF2=42+(8-EF)2,
解得:EF=5,
∴DE=EF=5.
∴CE=3.

练习册系列答案
相关题目
【题目】小颖和小红两名同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
①填空:此次试验中“5点朝上”的频率为________;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图法加以说明,并求出其概率.