题目内容
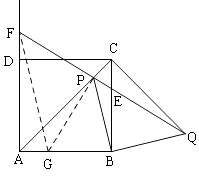
【题目】边长为2 ![]() 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE= ![]() BC;
BC;
(3)猜想PF与EQ的数量关系,并证明你的结论.
【答案】
(1)
证明:如图1,
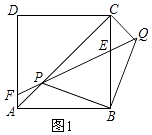
∵线段BP绕点B顺时针旋转90°得到线段BQ,
∴BP=BQ,∠PBQ=90°.
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°.
∴∠ABC=∠PBQ.
∴∠ABC﹣∠PBC=∠PBQ﹣∠PBC,即∠ABP=∠CBQ.
在△BAP和△BCQ中,
∵ 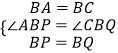 ,
,
∴△BAP≌△BCQ(SAS).
∴CQ=AP
(2)
解:如图1,

∵四边形ABCD是正方形,
∴∠BAC= ![]() ∠BAD=45°,∠BCA=
∠BAD=45°,∠BCA= ![]() ∠BCD=45°,
∠BCD=45°,
∴∠APB+∠ABP=180°﹣45°=135°,
∵DC=AD=2 ![]() ,
,
由勾股定理得:AC= ![]() =4,
=4,
∵AP=x,
∴PC=4﹣x,
∵△PBQ是等腰直角三角形,
∴∠BPQ=45°,
∴∠APB+∠CPQ=180°﹣45°=135°,
∴∠CPQ=∠ABP,
∵∠BAC=∠ACB=45°,
∴△APB∽△CEP,
∴ ![]() ,
,
∴ ![]() ,
,
∴y= ![]() x(4﹣x)=﹣
x(4﹣x)=﹣ ![]() x(0<x<4),
x(0<x<4),
由CE= ![]() BC=
BC= ![]() =
= ![]() ,
,
∴y=﹣ ![]() x=
x= ![]() ,
,
x2﹣4x=3=0,
(x﹣3)(x﹣1)=0,
x=3或1,
∴当x=3或1时,CE= ![]() BC;
BC;
(3)
解:结论:PF=EQ,理由是:
如图,当F在边AD上时,过P作PG⊥FQ,交AB于G,则∠GPF=90°,
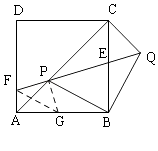
∵∠BPQ=45°,
∴∠GPB=45°,
∴∠GPB=∠PQB=45°,
∵PB=BQ,∠ABP=∠CBQ,
∴△PGB≌△QEB,
∴EQ=PG,
∵∠BAD=90°,
∴F、A、G、P四点共圆,
连接FG,
∴∠FGP=∠FAP=45°,
∴△FPG是等腰直角三角形,
∴PF=PG,
∴PF=EQ.
当F在AD的延长线上时,
如图,同理可得:PF=PG=EQ.
【解析】(1)证出∠ABP=∠CBQ,由SAS证明△BAP≌△BCQ可得结论;(2)如图1证明△APB∽△CEP,列比例式可得y与x的关系式,根据CE= ![]() BC计算CE的长,即y的长,代入关系式解方程可得x的值;(3)如图3,作辅助线,构建全等三角形,证明△PGB≌△QEB,得EQ=PG,由F、A、G、P四点共圆,得∠FGP=∠FAP=45°,所以△FPG是等腰直角三角形,可得结论.
BC计算CE的长,即y的长,代入关系式解方程可得x的值;(3)如图3,作辅助线,构建全等三角形,证明△PGB≌△QEB,得EQ=PG,由F、A、G、P四点共圆,得∠FGP=∠FAP=45°,所以△FPG是等腰直角三角形,可得结论.
如图4,当F在AD的延长线上时,同理可得结论.
【考点精析】关于本题考查的全等三角形的性质和等腰三角形的性质,需要了解全等三角形的对应边相等; 全等三角形的对应角相等;等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.

【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?