题目内容
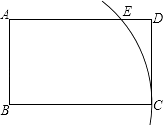
【题目】BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A.![]() 或2
或2 ![]()
B.![]() 或2
或2 ![]()
C.![]() 或2
或2 ![]()
D.![]() 或2
或2 ![]()
【答案】D
【解析】解:过B作直径,连接AC交AO于E,
∵点B为 ![]() 的中点,
的中点,
∴BD⊥AC,
①如图①,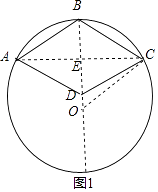
∵点D恰在该圆直径的三等分点上,
∴BD= ![]() ×2×3=2,
×2×3=2,
∴OD=OB﹣BD=1,
∵四边形ABCD是菱形,
∴DE= ![]() BD=1,
BD=1,
∴OE=2,
连接OD,
∵CE= ![]() =
= ![]() ,
,
∴边CD= ![]() =
= ![]() ;
;
如图②,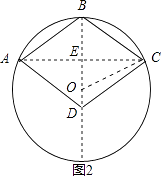
BD= ![]() ×2×3=4,
×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OD,
∵CE= ![]() =
= ![]() =2
=2 ![]() ,
,
∴边CD= ![]() =
= ![]() =2
=2 ![]() ,
,
故选D.
【考点精析】利用菱形的性质和圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动,某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |

(1)表中a= , b=;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.