题目内容
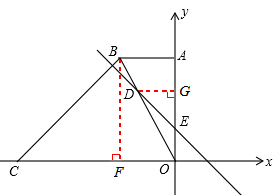
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 ,点C的坐标为(-18,0)。
,点C的坐标为(-18,0)。

(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式;
(3)若点P是(2)中直线DE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
 ,点C的坐标为(-18,0)。
,点C的坐标为(-18,0)。
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式;
(3)若点P是(2)中直线DE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
(1)(-6,12)(2)y=-x+4(3)结论:存在。点Q的坐标为:(2 ,-2
,-2  ),(-2
),(-2 ,2
,2  ),(4,4),(-2,2)
),(4,4),(-2,2)
 ,-2
,-2  ),(-2
),(-2 ,2
,2  ),(4,4),(-2,2)
),(4,4),(-2,2)解:(1)过点B作BF⊥x轴于F,
在Rt△BCF中
∵∠BCO=45°,BC=12 ,∴CF="BF=12" 。
,∴CF="BF=12" 。
∵C 的坐标为(-18,0),∴AB=OF=6。
∴点B的坐标为(-6,12)。
(2)过点D作DG⊥y轴于点G,
∵OD=2BD,∴OD= OB。
OB。
∵AB∥DG,∴△ODG∽△OBA 。
∵ ,AB=6,OA=12,∴DG=4,OG=8。∴D(-4,8),E(0,4)。
,AB=6,OA=12,∴DG=4,OG=8。∴D(-4,8),E(0,4)。
设直线DE解析式为y=kx+b(k≠0)
∴ ,解得
,解得 。∴直线DE解析式为y=-x+4。
。∴直线DE解析式为y=-x+4。
(3)结论:存在。
点Q的坐标为:(2 ,-2
,-2  ),(-2
),(-2 ,2
,2  ),(4,4),(-2,2)。
),(4,4),(-2,2)。
(1)构造等腰直角三角形BCF,求出BF、CF的长度,即可求出B点坐标。
(2)已知E点坐标,欲求直线DE的解析式,需要求出D点的坐标.构造△ODG∽△OBA,由线段比例关系求出D点坐标,从而可以求出直线DE的解析式。
(3)如图所示,符合题意的点Q有4个:

设直线y=-x+4分别与x轴、y轴交于点E、点F,
则E(0,4),F(4,0),OE=OF=4,EF=4 。
。
①菱形OEP1Q1,此时OE为菱形一边。
则有P1E=P1Q1=OE=4,P1F=EF-P1E=4 -4。
-4。
易知△P1NF为等腰直角三角形,
∴P1N=NF= P1F=4-2
P1F=4-2 。
。
设P1Q1交x轴于点N,则NQ1=P1Q1-P1N=4-(4-2 )=2
)=2 。
。
又ON=OF-NF=2 ,∴Q1(2
,∴Q1(2 ,-2
,-2 )。
)。
②菱形OEP2Q2,此时OE为菱形一边。此时Q2与Q1关于原点对称,∴Q2(-2 ,2
,2 )。
)。
③菱形OEQ3P3,此时OE为菱形一边。
此时P3与点F重合,菱形OEQ3P3为正方形,∴Q3(4,4)。
④菱形OP4EQ4,此时OE为菱形对角线。
由菱形性质可知,P4Q4为OE的垂直平分线,
由OE=4,得P4纵坐标为2,代入直线解析式y=-x+4得横坐标为2,则P4(2,2)。
由菱形性质可知,P4、Q4关于OE或x轴对称,∴Q4(-2,2)。
综上所述,存在点Q,使以O、E、P、Q为顶点的四边形是菱形,点Q的坐标为:
Q1(2 ,-2
,-2 ),Q2(-2
),Q2(-2 ,2
,2 ),Q3(4,4),Q4(-2,2)。
),Q3(4,4),Q4(-2,2)。

在Rt△BCF中
∵∠BCO=45°,BC=12
 ,∴CF="BF=12" 。
,∴CF="BF=12" 。 ∵C 的坐标为(-18,0),∴AB=OF=6。
∴点B的坐标为(-6,12)。
(2)过点D作DG⊥y轴于点G,
∵OD=2BD,∴OD=
 OB。
OB。∵AB∥DG,∴△ODG∽△OBA 。
∵
 ,AB=6,OA=12,∴DG=4,OG=8。∴D(-4,8),E(0,4)。
,AB=6,OA=12,∴DG=4,OG=8。∴D(-4,8),E(0,4)。设直线DE解析式为y=kx+b(k≠0)
∴
 ,解得
,解得 。∴直线DE解析式为y=-x+4。
。∴直线DE解析式为y=-x+4。(3)结论:存在。
点Q的坐标为:(2
 ,-2
,-2  ),(-2
),(-2 ,2
,2  ),(4,4),(-2,2)。
),(4,4),(-2,2)。(1)构造等腰直角三角形BCF,求出BF、CF的长度,即可求出B点坐标。
(2)已知E点坐标,欲求直线DE的解析式,需要求出D点的坐标.构造△ODG∽△OBA,由线段比例关系求出D点坐标,从而可以求出直线DE的解析式。
(3)如图所示,符合题意的点Q有4个:

设直线y=-x+4分别与x轴、y轴交于点E、点F,
则E(0,4),F(4,0),OE=OF=4,EF=4
 。
。①菱形OEP1Q1,此时OE为菱形一边。
则有P1E=P1Q1=OE=4,P1F=EF-P1E=4
 -4。
-4。易知△P1NF为等腰直角三角形,
∴P1N=NF=
 P1F=4-2
P1F=4-2 。
。设P1Q1交x轴于点N,则NQ1=P1Q1-P1N=4-(4-2
 )=2
)=2 。
。又ON=OF-NF=2
 ,∴Q1(2
,∴Q1(2 ,-2
,-2 )。
)。②菱形OEP2Q2,此时OE为菱形一边。此时Q2与Q1关于原点对称,∴Q2(-2
 ,2
,2 )。
)。③菱形OEQ3P3,此时OE为菱形一边。
此时P3与点F重合,菱形OEQ3P3为正方形,∴Q3(4,4)。
④菱形OP4EQ4,此时OE为菱形对角线。
由菱形性质可知,P4Q4为OE的垂直平分线,
由OE=4,得P4纵坐标为2,代入直线解析式y=-x+4得横坐标为2,则P4(2,2)。
由菱形性质可知,P4、Q4关于OE或x轴对称,∴Q4(-2,2)。
综上所述,存在点Q,使以O、E、P、Q为顶点的四边形是菱形,点Q的坐标为:
Q1(2
 ,-2
,-2 ),Q2(-2
),Q2(-2 ,2
,2 ),Q3(4,4),Q4(-2,2)。
),Q3(4,4),Q4(-2,2)。
练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目

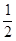 ∠COB
∠COB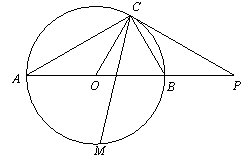
 ,
, ,
, ,过直角顶点
,过直角顶点 作
作 ,垂足为
,垂足为 ,再过
,再过 ,垂足为
,垂足为 ;过
;过 ,垂足为
,垂足为 ,再过
,再过 ,垂足为
,垂足为 ;……,这样一直做下去,得到了一组线段
;……,这样一直做下去,得到了一组线段 ,
, ,
, ,……,则第10条线段
,……,则第10条线段 .
.
 中,
中, 分别为
分别为 的中点,
的中点, 与
与 相交于点
相交于点 ,则
,则





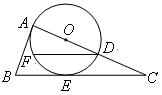
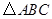 中,
中,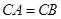 ,点
,点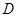 为
为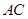 的中点,以
的中点,以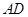 为直径的
为直径的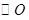 切
切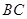 于点
于点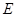 ,
,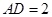 .
.
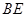 的长;(2)过点
的长;(2)过点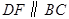 交
交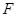 ,求
,求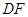 的长.
的长.