题目内容
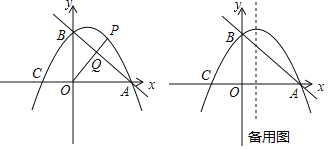
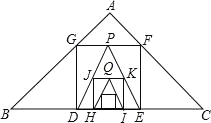
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
【答案】![]()
【解析】
首先根据勾股定理得出BC的长,进而利用等腰直角三角形的性质得出DE的长,再利用锐角三角函数的关系得出![]() ,即可得出正方形边长之间的变化规律,得出答案即可.
,即可得出正方形边长之间的变化规律,得出答案即可.
∵在Rt△ABC中,AB=AC=3![]() ,
,
∴∠B=∠C=45°,BC=![]() =6,
=6,
∵在△ABC内作第一个内接正方形DEFG;
∴EF=EC=DG=BD,
∴DE=![]() BC
BC
∴DE=2,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,
∴![]() ,
,
∴EI=![]() KI=
KI=![]() HI,
HI,
∵DH=EI,
∴HI=![]() DE=(
DE=(![]() )21×2,
)21×2,
则第n个内接正方形的边长为:2×(![]() )n1,
)n1,
∴则第2014个内接正方形的边长为2×(![]() )20141=2×
)20141=2×![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目