Question

【题目】已知抛物线y＝ax2+bx+c的对称轴为x＝﹣1，且过点（﹣3，0），（0，﹣3）．

（1）求抛物线的表达式．

（2）已知点（m，k）和点（n，k）在此抛物线上，其中m≠n，请判断关于t的方程t2+mt+n＝0是否有实数根，并说明理由．

Answer 1

【答案】（1）y＝x2+2x﹣3；（2）方程有两个不相等的实数根．

【解析】

（1）将已知点的坐标代入二次函数列出方程组，解之即可；

（2）因为（m，k），（n，k）是关于直线x＝﹣1的对称点，所以＝﹣1 即m＝﹣n﹣2，于是 b2﹣4ac＝m2﹣4n＝（﹣n﹣2）2﹣4n＝n2+4＞0，所以此方程有两个不相等的实数根．

（1）抛物线y＝ax2+bx+c的对称轴为x＝﹣1，且过点（﹣3，0），（0，3）

9a﹣3b+c＝0

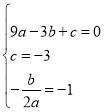
解得a＝1，b＝2，c＝﹣3

∴抛物线y＝x2+2x﹣3；

（2）∵点（m，k），（n，k）在此抛物线上，

∴（m，k），（n，k）是关于直线x＝﹣1的对称点，

∴＝﹣1 即m＝﹣n﹣2

b2﹣4ac＝m2﹣4n＝（﹣n﹣2）2﹣4n＝n2+4＞0

∴此方程有两个不相等的实数根．