Question

【题目】若四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫做这个四边形的“巧分线”，这个四边形叫“巧妙四边形”，若一个四边形有两条巧分线，则称为“绝妙四边形”．

（1）下列四边形一定是巧妙四边形的是　 　；（填序号点①平行四边形；②矩形；③菱形；④正方形．

初步应用

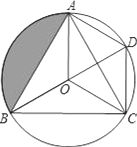
（2）在绝妙四边形ABCD中，AC垂直平分BD，若∠BAD＝80°，则∠BCD＝　 　；

深入研究

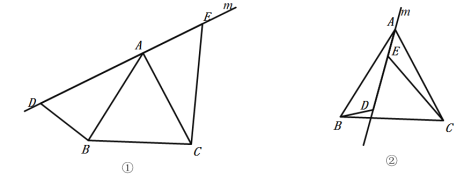
（3）如图，在梯形ABCD中，AD∥BC，AB＝AD＝CD，∠B＝72°．求证：梯形ABCD是绝妙四边形．

（4）在巧妙四边形ABCD中，AB＝AD＝CD，∠A＝90°，AC是四边形ABCD的巧分线，请直接写出∠BCD的度数．

Answer 1

【答案】（1）③④；（2）140°或80°或160°；（3）见解析；（4）∠BCD的度数是45°或135°或90°

【解析】

（1）由巧妙四边形的定义，即可得到菱形和正方形是巧妙四边形；

（2）根据绝妙四边形的定义可知：两条对角线都是巧分线，分情况画图进行计算可得结论；

（3）首先根据题意画出图形，然后分别证明两条对角线分成的三角形是等腰三角形即可；

（4）根据AC是四边形ABCD的巧分线，可知：△ACD和△ABC是等腰三角形，△ABC是等腰三角形时分三种情况画图进行讨论可得结论．

解：（1）∵菱形的四条边相等，

∴连接对角线能得到两个等腰三角形，

∴菱形是巧妙四边形；

正方形是特殊的菱形，所以正方形也是巧妙四边形；

故答案是：③④；

（2）分三种情况，

①当AC＝AD＝AB时，如图1，

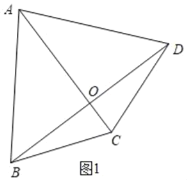
∵AC垂直平分BD，

∴AB＝AD，BC＝CD，AC⊥BD，

∴∠BAC＝∠DAC，

∵∠BAD＝80°，

∴∠BAC＝∠DAC＝40°，

∵AC＝AD＝AB，

∴∠ACD＝∠ADC＝∠ACB＝∠ABC＝＝70°，

∴∠BCD＝2∠ACD＝140°；

②当AD＝CD，AB＝BC时，如图2，

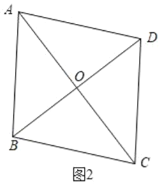
∵AC垂直平分BD，

∴AB＝AD，BC＝CD，AC⊥BD，

∴AB＝AD＝CD＝BC，

∴四边形ABCD是菱形，

∴∠BCD＝∠BAD＝80°；

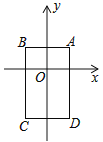
③在四边形ABCD中，AC＝CD＝BC，如图3，

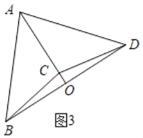
∴∠CAD＝∠ADC＝40°

∴∠ACD＝∠ACB＝100°

∴∠BCD＝360°﹣100°﹣100°＝160°；

综上，∠BCD＝140°或80°或160°；

故答案为：140°或80°或160°；

（3）如图4，连接AC与BD，交于点O，

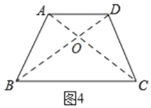
在梯形ABCD中，AB＝CD，

∴∠ABC＝∠DCB＝72°，

∵AD∥BC，

∴∠BAD＝∠ADC＝108°，

∵AB＝AD＝CD，

∴△ABD是等腰三角形，∠ABD＝∠ADB＝36°，

∴∠DBC＝72°﹣36°＝36°，∠BDC＝108°﹣36°＝72°＝∠DCB，

∴△BDC也是等腰三角形，

∴对角线BD叫做这个四边形ABCD的“巧分线”，

同理可得△ADC和△ACB也是等腰三角形，

∴对角线AC叫做这个四边形ABCD的“巧分线”，

∴梯形ABCD是绝妙四边形；

（4）∵AC是四边形ABCD的巧分线，

∴△ACD和△ABC是等腰三角形，

①当AC＝BC时，如图5，过C作CH⊥AB于H，过C作CG⊥AD，交AD的延长线于G，

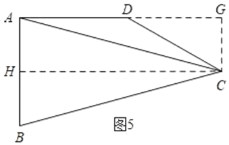
∵∠HAD＝∠AHC＝∠G＝90°，

∴四边形AHCG是矩形，

∴AH＝CG＝AB＝CD，

∴∠CDG＝30°，

∴∠ADC＝150°，

∴∠DAC＝∠DCA＝15°，

∵∠DAB＝90°，

∴∠CAB＝∠B＝75°，

∴∠ACB＝30°，

∴∠BCD＝30°+15°＝45°；

②当AC＝AB时，如图6，

∵AC＝AB＝AD＝CD，

∴△ACD是等边三角形，

∴∠CAD＝∠ACD＝60°，

∵∠BAD＝90°，

∴∠BAC＝30°，

∵AB＝AC，

∴∠ACB＝75°，

∴∠BCD＝75°+60°＝135°；

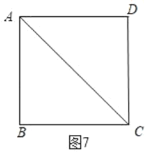
③当AB＝BC时，如图7，此时∠BCD＝90°

综上，∠BCD的度数是45°或135°或90°．