题目内容
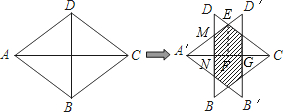
如图,菱形ABCD中,AC=8,BD=6,将△ABD沿AC方向向右平移到△A′B′D′的位置,若平移距离为2,则阴影部分的面积为_________

7.5.
试题分析:首先设A′D′交CD于点E,交BD于点M,BD交A′C于点N,过点E作EF⊥A′C于点F,由平移的性质与菱形的性质,易求得A′G,A′N,A′F与D′G的长,易得BD∥EF∥B′D′,即可求得△A′MN∽△A′D′G,△A′EF∽△A′D′G,然后由相似三角形的对应边成比例,即可求得MN与EF的长,继而求得梯形MNFE的面积,则可求得答案.
试题解析:根据题意得:NG=2,
设A′D′交CD于点E,交BD于点M,BD交A′C于点N,过点E作EF⊥A′C于点F,
由平移的性质可得:NF=GF=
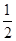 NG=1,
NG=1,∵菱形ABCD中,AC=8,BD=6,
∴A′G=
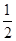 AC=4,D′G=
AC=4,D′G=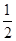 BD=3,B′D′⊥A′C,BD⊥A′C,
BD=3,B′D′⊥A′C,BD⊥A′C,∴A′N-A′G=NG=4-2=2,A′F=A′G-GF=4-1=3,BD∥EF∥B′D′,
∴△A′MN∽△A′D′G,△A′EF∽△A′D′G,
∴
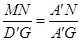 ,
,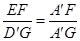 ,
,即
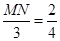 ,
,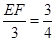 ,
,∴MN=
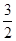 ,EF=
,EF=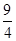 ,
,∴S梯形MNFE=
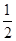 ×(MN+EF)×HF=
×(MN+EF)×HF=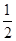 ×(
×(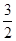 +
+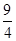 )×1=
)×1=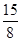 ,
,∴S阴影=4S梯形MNFE=4×
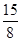 =7.5.
=7.5.
练习册系列答案
相关题目

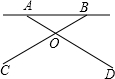

 P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.
P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.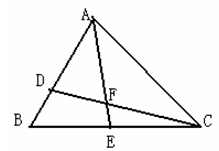
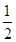 B、1 C、
B、1 C、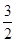 D、2
D、2 ,相似比为1:2,则
,相似比为1:2,则 与
与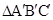 的面积的比为( )
的面积的比为( ) 的值为 ;
的值为 ;
