题目内容
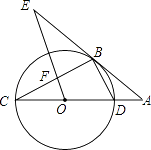
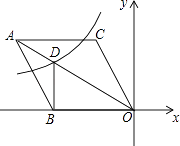
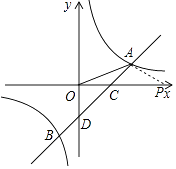
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y= ![]() 的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.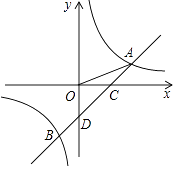
(1)求a,k的值及点B的坐标;
(2)直接写出不等式ax﹣1≥ ![]() 的解集;
的解集;
(3)在x轴上存在一点P,使得△POA与△OAC相似(不包括全等),请你求出点P的坐标.
【答案】
(1)解:把A(3,1)代入一次函数y=ax﹣1与反比例函数y= ![]() 的解析式中,得到a=
的解析式中,得到a= ![]() ,k=3,
,k=3,
由  ,解得
,解得 ![]() 或
或 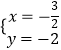 ,
,
∴B(﹣ ![]() ,﹣2).
,﹣2).
(2)解:观察图象可知不等式ax﹣1≥ ![]() 的解集为﹣
的解集为﹣ ![]() ≤x<0或x≥3.
≤x<0或x≥3.
(3)解:如图当∠APO=∠OAC时,∵∠AOC=∠POA,
∴△AOC∽△POA,
∴ ![]() =
= ![]() ,
,
∴OA2=OCOP,
易知OA= ![]() ,OC=
,OC= ![]() ,
,
∴10= ![]() OP,
OP,
∴OP= ![]() ,
,
∴P( ![]() ,0).
,0).
∴满足条件的点P的坐标为( ![]() ,0).
,0).
【解析】(1)把A(3,1)代入一次函数y=ax﹣1与反比例函数y= ![]() 的解析式中,可得a=
的解析式中,可得a= ![]() ,k=3,构建方程组即可求出点B坐标;(2)观察图象一次函数的图象在反比例函数的图象的上方即可,写出相应的自变量的取值范围即可;(3)如图当∠APO=∠OAC时,又∠AOC=∠POA,推出△AOC∽△POA,可得
,k=3,构建方程组即可求出点B坐标;(2)观察图象一次函数的图象在反比例函数的图象的上方即可,写出相应的自变量的取值范围即可;(3)如图当∠APO=∠OAC时,又∠AOC=∠POA,推出△AOC∽△POA,可得 ![]() =
= ![]() ,即OA2=OCOP,由此求出OP即可解决问题;
,即OA2=OCOP,由此求出OP即可解决问题;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目