题目内容
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
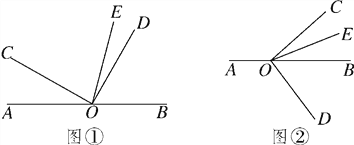
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
【答案】(1)15°;(2)![]() ;(3)①∠AOC=2∠DOE;②4∠DOE-5∠AOF=180°.
;(3)①∠AOC=2∠DOE;②4∠DOE-5∠AOF=180°.
【解析】试题分析:(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
②设∠DOE=x,∠AOF=y,根据已知和:∠AOC-4∠AOF=2∠BOE+∠AOF,得出4x-5y=180,从而得出结论.
解:(1)由已知得∠BOC=180°-∠AOC=150°,又∠COD是直角,OE平分∠BOC,∴∠DOE=∠COD-![]() ∠BOC=90°-
∠BOC=90°-![]() ×150°=15°.
×150°=15°.
(2)∠DOE=![]() a. 解析:由(1)知∠DOE=∠COD-
a. 解析:由(1)知∠DOE=∠COD-![]() ∠BOC=90°,∴∠DOE=90°-
∠BOC=90°,∴∠DOE=90°-![]() (180°-∠AOC)=
(180°-∠AOC)=![]() ∠AOC=
∠AOC=![]() α.
α.
(3)①∠AOC=2∠DOE.理由如下:
∵∠COD是直角,OE平分∠BOC,
∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),∴∠AOC=2∠DOE.
②4∠DOE-5∠AOF=180°.
理由如下:设∠DOE=x,∠AOF=y,
∴∠AOC-4∠AOF=2∠DOE-4∠AOF=2x-4y,2∠BOE+∠AOF=2(90°-x)+y=180°-2x+y,
∴2x-4y=180°-2x+y,即4x-5y=180°,
∴4∠DOE-5∠AOF=180°.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案