题目内容
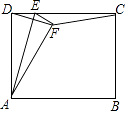
【题目】如图，这四边行ABCD中，点M、N分别在AB，CD边上，将四边形ABCD沿MN翻折，使点B、C分别在四边形外部点B1 ， C1处，则∠A+∠B1+∠C1+∠D= ．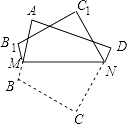 
【答案】360°
【解析】解：∵将四边形ABCD沿MN翻折，使点B、C分别在四边形外部点B1，C1处，
∴∠B=∠B1，∠C=∠C1，
∵∠A+∠B+∠C+∠D=360°，
∴∠A+∠B1+∠C1+∠D=360°，
所以答案是：360°．
【考点精析】根据题目的已知条件，利用多边形内角与外角和翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
相关题目
