Question

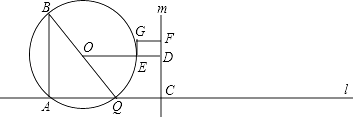
【题目】如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，∠AEO=∠C，OE交BC于点F．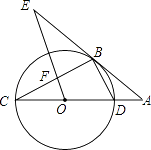

（1）求证：OE∥BD；
（2）当⊙O的半径为5，sin∠DBA= 时，求EF的长．

Answer 1

【答案】
（1）证明：连接OB，

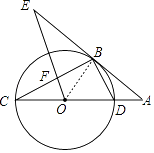
∵CD为⊙O的直径，

∴∠CBD=∠CBO+∠OBD=90°，

∵AE是⊙O的切线，

∴∠ABO=∠OBD+∠ABD=90°，

∴∠ABD=∠CBO，

∵OB、OC是⊙O的半径，

∴OB=OC．

∴∠C=∠CBO，

∴∠C=∠ABD，

∵∠E=∠C，

∴∠E=∠ABD，

∴OE∥BD

（2）解：由（1）可得sin∠C=∠DBA= ，

在Rt△OBE中，sin∠C= ，OC=5

∴BD=4，

∵∠CBD=∠EBO=90°，∠E=∠C，

∴△CBD∽△EBO．

∴ = ，

∴EO= ，

∵OE∥BD，CO=OD，

OF= BD=2，

∴CF=FB．

EF=OE﹣OF=

【解析】（1） 连接OB，由直径所对的圆周角是直角得出∠CBD=∠CBO+∠OBD=90°，又由切线的性质定理得出∠ABO=∠OBD+∠ABD=90°，进而得出∠ABD=∠CBO，由同圆的半径相等得出∠C=∠CBO，进而得出∠C=∠ABD，∠E=∠ABD，由平行线的判断定理得出结论；（2）由（1）可得sin∠C=∠DBA在在Rt△OBE中根据sin∠C得出BD的长度，进而判断出△CBD∽△EBO．由相似三角形的性质得出OE的长度，最后由中位线的判断得出CF=FB．进而得出结论。
【考点精析】本题主要考查了平行线的判定和圆周角定理的相关知识点，需要掌握同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．