题目内容
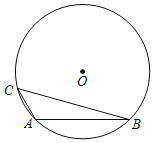
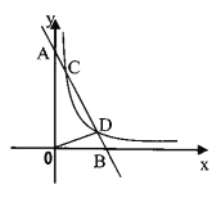
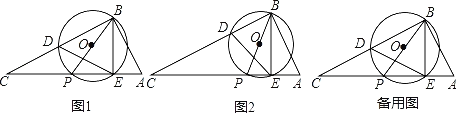
【题目】如图1,Rt△ABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点为E(点E在点P右侧),连结DE、BE,已知AB=3,BC=6.
(1)求线段BE的长;
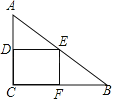
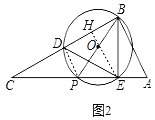
(2)如图2,若BP平分∠ABC,求∠BDE的正切值;
(3)是否存在点P,使得△BDE是等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.
【答案】(1)BE=![]() ;(2)tan∠BDE=3;(3)符合条件的CP的长为3
;(2)tan∠BDE=3;(3)符合条件的CP的长为3![]() ﹣3或
﹣3或![]() 或
或![]() .
.
【解析】
(1)求出AC=3![]() ,由三角形ABC的面积可求出BE的长;
,由三角形ABC的面积可求出BE的长;
(2)连接DP,证明△CPD∽△CAB,得出![]() =2,设DP=BD=x,则CD=2x,由CB=3x=6,得出x=2,根据tan∠BDE=tan∠BPE可得出答案;
=2,设DP=BD=x,则CD=2x,由CB=3x=6,得出x=2,根据tan∠BDE=tan∠BPE可得出答案;
(3)分三种情况,求出CP=![]() CD,求出CD,可得出答案.
CD,求出CD,可得出答案.
解:(1)∵∠ABC=90°,AB=3,BC=6,
∴AC=![]() =
=![]() =3
=3![]() ,
,
∵BP为⊙O的直径,
∴∠BEP=90°,
∴BE⊥AC,
∵S△ABC=![]() ×AB×AC,
×AB×AC,
∴BE=![]() ;
;
(2)∵BP平分∠ABC,
∴∠DBP=![]() ∠ABC=45°,
∠ABC=45°,
连接DP,如图1,
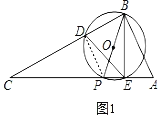
∵BP为⊙O的直径,
∴∠DBP=∠DPB=45°,
∴可设DP=BD=x,
∵∠CDP=∠ABC=90°
∴PD∥AB,
∴△CPD∽△CAB,
∴![]() =2,
=2,
∴CD=2x,
∴CB=3x=6,
∴x=2,
∴DP=BD=2,CD=4,
∴CP=![]() =
=![]() =2
=2![]() ,
,
∴CE=![]() =
=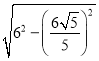 =
=![]() ,
,
∴tan∠BDE= tan∠BPE=![]() =
=![]() =3.
=3.
(3)解:存在这样的点P.
由△DCP∽△BCA,得,![]() ,
,
∴CP=![]() CD,
CD,
若△BDE是等腰三角形,可分三种情况:
①当BD=BE时,BD=BE=![]() ,
,
∴CD=BC﹣BD=6﹣![]() ,
,
∴CP=![]() =3
=3![]() ﹣3.
﹣3.
②当BD=DE时,此时点D是Rt△CBE斜边的中点,
∴CD=![]() BC=3,
BC=3,
∴CP=![]() ;
;
③当DE=BE时,作EH⊥BC于点H,则H是BD的中点,
∵∠ABC=∠EHC=90°,
∴EH∥AB,
∴![]() ,
,
又∵AE=AC﹣CE=3![]() ﹣
﹣![]() =
=![]() ,
,
∴BH=DH=![]() =
=![]() ,
,
∴CD=6﹣![]() =
=![]() ,
,
∴CP=![]() .
.
综上所述,△BDE是等腰三角形,符合条件的CP的长为3![]() ﹣3或
﹣3或![]() 或
或![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案