题目内容
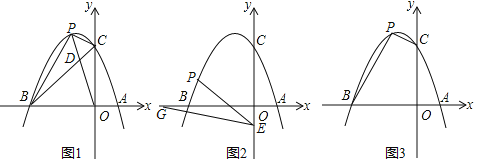
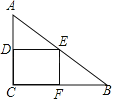
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E在边AB上,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.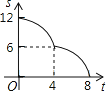 B.
B.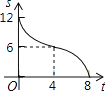 C.
C. D.
D.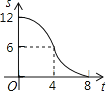
【答案】D
【解析】
证明△DEF≌△BFE(AAS),则![]() ;分0≤t≤4、4<t≤8两种情况,分别求出函数表达式,即可求解.
;分0≤t≤4、4<t≤8两种情况,分别求出函数表达式,即可求解.
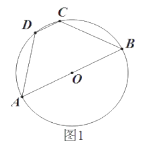
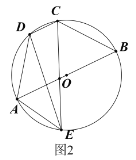
如图1,连接DF,
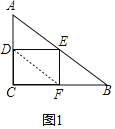
∵![]() ,即tanB=tan∠EDF,
,即tanB=tan∠EDF,
∴∠B=∠EDF,而∠DEF=∠EFB=90°,EF=EF,
∴△DEF≌△BFE(AAS),
∴![]() ,即点F是BC的中点,
,即点F是BC的中点,
![]() ,
,
故矩形DCFE的面积为3×4=12;
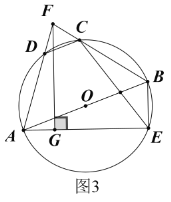
当0≤t≤4时,如图2,
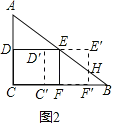
设直线AB交D′C′F′E′于点H,
则EE′=t,![]() ,
,
![]() ,
,
该函数为开口向下的抛物线,当t=4时,S=6;
当4<t≤8时,
同理可得:![]() ,
,
该函数为开口向上的抛物线;
故选:D.

【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数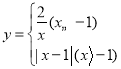 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
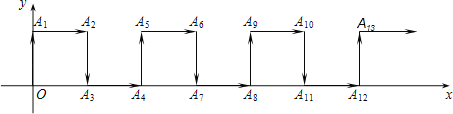
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
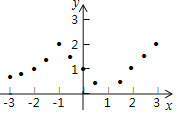
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:
80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
|
| 5 |
|
|
|
|
|
|
|
| 2 |
八、九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 |
|
|
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)八年级王宇和九年级程义的分数都为80分,请判断王宇、程义在各自年级的排名哪位更靠前?请简述你的理由;
(3)八年级被抽取的20名学生中,获得![]() 等和
等和![]() 等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为
等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为![]() 等的概率.
等的概率.