题目内容
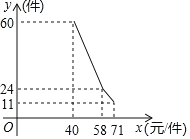
【题目】在“前线医护人员”和全国人民的共同努力下，疫情得到了有效控制，宁波各大企业复工复产有序进行．为了实现员工“一站式”返岗，宁波某企业打算租赁5辆客车前往宁波东站接员工返岗．已知现有A、B两种客车，A型客车的载客量为45人/辆，每辆租金为400元；B型客车的载客量为30人/辆，每辆租金为280元．设租用A型客车为x辆，所需费用为y元．
（1）求y关于x的函数解析式；
（2）若该企业需要接的员工有205人，请求出租车费用最小值，并写出对应的租车方案．
【答案】（1）y＝120x+1400；（2）方案为租用A型客车4辆，租用B型客车1辆．
【解析】
（1）根据总费用＝A型看成的费用+B型客车的费用，即可解决问题．
（2）列出不等式求出x的范围，再根据x是整数，求出x的值，根据一次函数的性质即可解决问题．
解：（1）设租用A型客车为x辆，则租用B型客车为（5﹣x）辆，
由题意得：y＝400x+280（5﹣x）＝120x+1400．
（2）由题意：45x+30（5﹣x）≥205，解得x≥
，
而费用y＝120x+1400，
∵x为整数，x取最小，费用y最低，
∴x＝4，
∴方案为租用A型客车4辆，租用B型客车1辆．
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数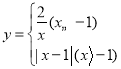
的图象与性质．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．
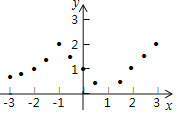
（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点
，
，
，
在函数图象上，
，
；（填“＞”，“＝”或“＜”）
②当函数值
时，求自变量x的值；
③在直线
的右侧的函数图象上有两个不同的点
，
，且
，求
的值；
④若直线
与函数图象有三个不同的交点，求a的取值范围．
