题目内容
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y=![]() (k≠0)经过点C,则k的值为( )
(k≠0)经过点C,则k的值为( )
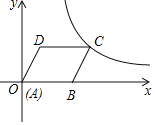
A.12B.15C.20D.32
【答案】D
【解析】
分别过点D,C作x轴的垂线,垂足为M,N,先利用勾股定理求出菱形的边长,再利用Rt△ODM≌Rt△BCN得出BN=OM,则可确定点C的坐标,将C点坐标代入反比例函数解析式中即可求出k的值.
如图,分别过点D,C作x轴的垂线,垂足为M,N,

∵点D的坐标是 (3,4),
∴OM=3,DM=4,
在Rt△OMD中,
OD=![]()
∵四边形ABCD为菱形,
∴OD=CB=OB=5,DM=CN=4,
∴Rt△ODM≌Rt△BCN(HL),
∴BN=OM=3,
∴ON=OB+BN=5+3=8,
又∵CN=4,
∴C(8,4),
将C(8,4)代入![]()
得,k=8×4=32,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目