题目内容
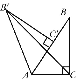
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt△AB'C'可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段B'C的长为______.
【答案】3
【解析】
作B′D⊥AC于D，构造直角三角形，利用旋转性质得AB′=AB=6，∠B′AB=60°，
所以，∠DAB′=180°-60°-60°=60°，在Rt△DAB′中，AD=
AB′=3，B′D=
AD=3，可得CD=DA+AC=6，根据勾股定理得B′C=
= 3.
作B′D⊥AC于D，如图，
∵∠ACB=90°，∠BAC=60°，AB=6，
∴AC=AB=3，
∵RtAB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的，
∴AB′=AB=6，∠B′AB=60°，
∴∠DAB′=180°-60°-60°=60°，
在Rt△DAB′中，∠DB′A=30°，AB′=6，
∴AD=AB′=3，B′D=AD=3，
∴CD=DA+AC=6，
在Rt△CDB′中，B′C== 3.
故答案为：3
练习册系列答案
优学名师名题系列答案
相关题目
