题目内容
【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”,这条中线为“匀称中线”.
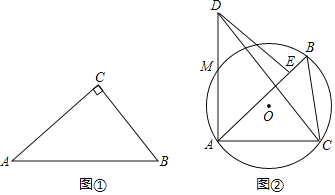
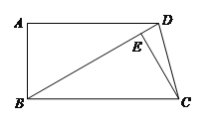
(1)如图①,在Rt△ABC中,∠C=90°,AC>BC,若Rt△ABC是“匀称三角形”.
①请判断“匀称中线”是哪条边上的中线,
②求BC:AC:AB的值.
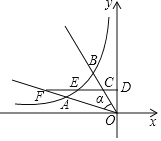
(2)如图②,△ABC是⊙O的内接三角形,AB>AC,∠BAC=45°,S△ABC=2![]() ,将△ABC绕点A逆时针旋转45°得到△ADE,点B的对应点为D,AD与⊙O交于点M,若△ACD是“匀称三角形”,求CD的长,并判断CM是否为△ACD的“匀称中线”.
,将△ABC绕点A逆时针旋转45°得到△ADE,点B的对应点为D,AD与⊙O交于点M,若△ACD是“匀称三角形”,求CD的长,并判断CM是否为△ACD的“匀称中线”.
【答案】(1)① “匀称中线”是BE,它是AC边上的中线,②BC:AC:AB=![]() ;(2)CD=
;(2)CD=![]() a,CM不是△ACD的“匀称中线”.理由见解析.
a,CM不是△ACD的“匀称中线”.理由见解析.
【解析】
(1)①先作出Rt△ABC的三条中线AD、BE、CF,然后利用匀称中线的定义分别验证即可得出答案;
②设AC=2a,利用勾股定理分别把BC,AB的长度求出来即可得出答案.
(2)由②知:AC:AD:CD=![]() ,设AC=
,设AC=![]() ,则AD=2a,CD=
,则AD=2a,CD=![]() ,过点C作CH⊥AB,垂足为H,利用
,过点C作CH⊥AB,垂足为H,利用![]() 的面积建立一个关于a的方程,解方程即可求出CD的长度;假设CM是△ACD的“匀称中线”,看能否与已知的定理和推论相矛盾,如果能,则说明假设不成立,如果不能推出矛盾,说明假设成立.
的面积建立一个关于a的方程,解方程即可求出CD的长度;假设CM是△ACD的“匀称中线”,看能否与已知的定理和推论相矛盾,如果能,则说明假设不成立,如果不能推出矛盾,说明假设成立.
(1)①如图①,作Rt△ABC的三条中线AD、BE、CF,
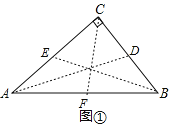
∵∠ACB=90°,
∴CF=![]() ,即CF不是“匀称中线”.
,即CF不是“匀称中线”.
又在Rt△ACD中,AD>AC>BC,即AD不是“匀称中线”.
∴“匀称中线”是BE,它是AC边上的中线,
②设AC=2a,则CE=a,BE=2a,
在Rt△BCE中∠BCE=90°,
∴BC=![]() ,
,
在Rt△ABC中,AB=![]() ,
,
∴BC:AC:AB=![]()
(2)由旋转可知,∠DAE=∠BAC=45°.AD=AB>AC,
∴∠DAC=∠DAE+∠BAC=90°,AD>AC,
∵Rt△ACD是“匀称三角形”.
由②知:AC:AD:CD=![]()
设AC=![]() ,则AD=2a,CD=
,则AD=2a,CD=![]() ,
,
如图②,过点C作CH⊥AB,垂足为H,则∠AHC=90°,
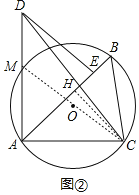
∵∠BAC=45°,
∴![]()
∵![]()
解得a=2,a=﹣2(舍去),
∴![]()
判断:CM不是△ACD的“匀称中线”.
理由:假设CM是△ACD的“匀称中线”.
则CM=AD=2AM=4,AM=2,
∴![]()
又在Rt△CBH中,∠CHB=90°,CH=![]() ,BH=4-
,BH=4-![]() ,
,
∴![]()
即![]()
这与∠AMC=∠B相矛盾,
∴假设不成立,
∴CM不是△ACD的“匀称中线”.