Question

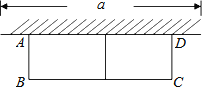
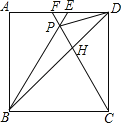
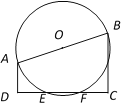
【题目】如图，梯形ABCD中，AD∥BC，∠ADC=90，AD= 2，BC= 4，.以AB为直径作⊙O，交边DC于E、F两点.

(1)求证：DE=CF.

(2)求直径AB的长.

Answer 1

【答案】(1)证明见解析；(2)AB=.

【解析】

（1）首先根据AD∥BC，∠ADC=90，OH⊥DC，得出AD∥OH∥BC，进而根据OA=OB得出DH=HC，然后根据垂径定理得出EH = HF，进而得出DE=CF；

（2）首先根据∠AGB =∠BCN = 90°，得出AG∥DC，然后根据AD∥BC，得出AD=CG.，进而得出BG，再根据三角函数得出AG，最后根据勾股定理得出AB.

(1)过点O作OH⊥DC，垂足为H.

∵AD∥BC，∠ADC=90，OH⊥DC，

∴∠BCN=∠OHC=∠ADC =90.

∴AD∥OH∥BC.

又∵OA=OB.

∴DH=HC.

∵OH⊥DC，OH过圆心，

∴EH = HF.

∴DH-EH =HC-HF.

即：DE=CF.

(2)过点A作AG⊥BC，垂足为点G，∠AGB = 90°，

∵∠AGB =∠BCN = 90°，

∴AG∥DC.

∵AD∥BC，

∴AD=CG.

∵AD= 2，BC= 4，

∴BG= BC-CG =2.

在Rt△AGB中，∵，

∴.

在Rt△AGB中，

∴AB=.