题目内容
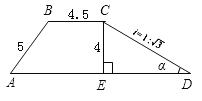
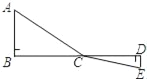
【题目】阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为![]() .然后利用几何知识可知:当A、C、E在一条直线上时,x=
.然后利用几何知识可知:当A、C、E在一条直线上时,x=![]() 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式![]() 的最小值为_____.
的最小值为_____.
【答案】4![]()
【解析】
根据已知图象,重新构造直角三角形,利用三角形相似得出CD的长,进而利用勾股定理得出最短路径问题.
如图所示:
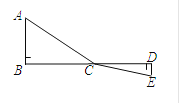
C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,
若AB=5,DE=3,BD=12,
当A,C,E,在一条直线上,AE最短,
∵AB⊥BD,ED⊥BD,
∴AB∥DE,
∴△ABC∽EDC,
∴![]() ,
,
∴![]() ,
,
解得:DC=![]() .
.
即当x=![]() 时,代数式
时,代数式![]() 有最小值,
有最小值,
此时为:![]() .
.
故答案是:4![]() .
.

练习册系列答案
相关题目