题目内容
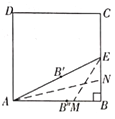
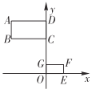
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.在运动的过程中,写出以P、O、E为顶点的三角形与△ABE相似时t的值为_____________
【答案】![]()
【解析】
本题需先证出△BCP∽△BAE ,求出AE=![]() t,由△POE和△BAE相似,再间接得到△POE∽△PCB ,根据相似三角形写出比例式求出t的值.
t,由△POE和△BAE相似,再间接得到△POE∽△PCB ,根据相似三角形写出比例式求出t的值.
∴∠ABE+∠ABP=90°,
∠PBC+∠ABP=90°,
∴∠ABE=∠PBC,
∵∠BAE=∠BCP=90°,
∴△BCP∽△BAE,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() t,
t,
∵若△POE∽△PCB,
∴![]() ,
,
∴![]() ,
,
∴t1=![]() ,
,
t2=![]() (舍去).
(舍去).
当点P在y轴负半轴时,若△POE∽△EAB,则有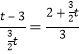 ,无解.
,无解.
若△POE∽△BAE,则有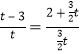 ,解得t=3+
,解得t=3+![]() 或t+3-
或t+3-![]() (舍去)
(舍去)
故答案为:![]() .
.

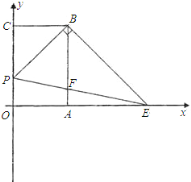
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.