题目内容
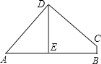
【题目】已知矩形
和点
，当点在
上任一位置（如图
所示）时，易证得结论：
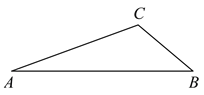
，请你探究：当点分别在图
、图
中的位置时，
、
、
和
又有怎样的数量关系请你写出对上述两种情况的探究结论，并利用图证明你的结论．
答：对图的探究结论为________；
对图的探究结论为________；
【答案】
【解析】
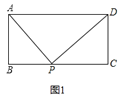
结论均是：．如图2，过点P作MN∥AB，交AD于点M，交BC于点N，可得四边形ABNM和四边形NCDM均为矩形，根据（1）中的结论可得，在矩形ABNM中有PA2+PN2=PB2+PM2①，在矩形NCDM中有PC2+PM2=PD2+PN2②， 利用①+②即可证得结论；如图3，过点P作MN∥AB，交AB的延长线于点M，交CD的延长线于点N，用上面的方法解决即可.
结论均是：．
（1）如图2，过点P作MN∥AB，交AD于点M，交BC于点N，
∴四边形ABNM和四边形NCDM均为矩形，
根据（1）中的结论可得，
在矩形ABNM中可得：PA2+PN2=PB2+PM2①，
在矩形NCDM中可得：PC2+PM2=PD2+PN2②，
①+②得：PA2+PN2+PC2+PM2=PB2+PM2+PD2+PN2，
∴PA2+PC2=PB2+PD2．
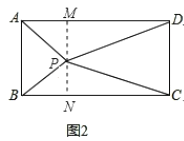
（2）如图3，过点P作MN∥AB，交AB的延长线于点M，交CD的延长线于点N，
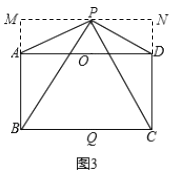
∴四边形BCNM和四边形ADNM均为矩形，
同样根据（1）中的结论可得，
在矩形BCNM中可得：PC2+PM2=PB2+PN2①，
在矩形ADNM中可得：PA2+PN2=PD2+PM2②，
①+②得：PA2+PN2+PC2+PM2=PD2+PM2+PB2+PN2，
∴PA2+PC2=PB2+PD2．
故答案为： ； .
练习册系列答案
阳光课堂课时作业系列答案
相关题目
